In This Topic
Confidence level
Because data samples are random, it is unlikely that two samples from the same population will yield identical tolerance intervals. But, if you collect many samples, a certain percentage of the resulting tolerance intervals will contain the minimum proportion of the population that you specify.
Note
You can specify the confidence level for the analysis in the Options dialog box. Minitab displays the target confidence level in the Methods table. By default, the confidence level is 95%. For the nonparametric method, Minitab calculates the achieved confidence level. The achieved confidence level is the exact confidence level that Minitab calculates. The achieved confidence level is usually greater than or equal to the target confidence level, unless your sample size is too small.
Percent of population in the interval
N
Mean
The mean summarizes the sample values with a single value that represents the center of the data. The mean is the average of the data, which is the sum of all the observations divided by the number of observations.
StDev
The standard deviation is the most common measure of dispersion, or how spread out the data are from the mean.
A larger standard deviation indicates that your data are spread more widely around the mean and will result in a wider tolerance interval. A smaller standard deviation indicates that your data are distributed more closely around the mean and will result in a narrower tolerance interval.
Normal method
Tolerance intervals are a range of values for a specific quality characteristic of a product that likely covers a specified percentage of future product output. Use the normal method tolerance interval if you can safely assume that your sample comes from a normally distributed population.
If your data follow a normal distribution, then the normal method is more precise and economical than the nonparametric method. The normal method allows you to achieve smaller margins of error with fewer observations.
The normal method is not robust to severe departures from normality. If you are unsure of the parent distribution, or you know that the parent distribution is not normal, then use the nonparametric method.
Interpretation
- Two-sided
- Use a two-sided interval to determine the interval that contains a certain percentage of the population measurements.
- Upper bound
- Use an upper bound to determine the interval that indicates that a certain percentage of population measurements will not be greater than an upper limit.
- Lower bound
- Use a lower bound to determine the interval that indicates that a certain percentage of population measurements will not be less than a lower limit.
Nonparametric method
Tolerance intervals are a range of values for a specific quality characteristic of a product that likely covers a specified proportion of future product output. If you cannot safely assume that your sample comes from a normally distribution population, you must use the nonparametric method tolerance interval.
The nonparametric method requires only that the data are continuous. However, the nonparametric method requires large sample sizes for the results to be accurate. If your sample size is not large enough, the nonparametric interval is a non-informative interval that ranges from negative infinity to infinity. In this case, Minitab displays a finite interval based on the range of your data. As a result, the achieved confidence level is much lower than the target confidence level.
Interpretation
- Two-sided
- Use a two-sided interval to determine the interval that contains a certain percentage of the population measurements.
- Upper bound
- Use an upper bound to determine the interval that indicates that a certain percentage of population measurements will not be greater than an upper limit.
- Lower bound
- Use a lower bound to determine the interval that indicates that a certain percentage of population measurements will not be less than a lower limit.
Achieved confidence
For the nonparametric method, Minitab calculates the achieved confidence level. This is the exact confidence level obtained from your sample. It will generally be greater than or equal to the target confidence level, unless your sample size is too small.
Interpretation
- Two-sided
- Use a two-sided interval to determine the interval that contains a certain percentage of the population measurements.
- Upper bound
- Use an upper bound to determine the interval that indicates that a certain percentage of population measurements will not be greater than an upper limit.
- Lower bound
- Use a lower bound to determine the interval that indicates that a certain percentage of population measurements will not be less than a lower limit.
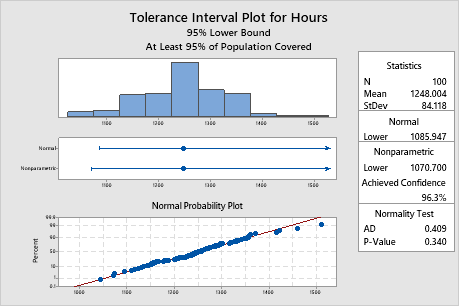
Tolerance interval plot
- Histogram: Shows the distribution of your sample data. Each bar on the histogram represents the frequency of data within an interval.
- Interval plots: Show the mean and the upper and/or lower bounds of the tolerance interval for each method. A vertical line at the end of the interval represents a bound, and an arrow indicates that no bound for that side of the interval exists.
- Normal probability plot: Shows how well your data fit the normal distribution. If your data are normally distributed, then the data points on the probability plot form a straight line.
- Statistics table: Displays the sample size, mean, and standard deviation.
- Normal table: Displays the upper and/or lower bounds of the normal method tolerance interval.
- Nonparametric table: Displays the upper and/or lower bounds of the nonparametric method tolerance interval, and the achieved confidence level.
- Normality Test table: Shows the p-value and the Anderson-Darling normality test value. To determine whether you can assume that the data follow a normal distribution, compare the p-value from the normality test to the significance level (α). If the p-value is less than or equal to the significance level, you can conclude that your data do not follow a normal distribution. In this case, you must use the nonparametric method tolerance interval.
Interpretation
The normal probability plot shows that the plotted points form an approximate straight line, which indicates that the data follow a normal distribution. Also, the p-value for the normality test is 0.340, which is greater than the significance level (α = 0.05). Thus, there is not enough evidence to conclude that the data do not follow a normal distribution. The engineer can use the normal method results.
The normal lower bound is 1085.947, so the engineer is 95% confident that at least 95% of all the light bulbs exceed approximately 1086 hours of burn time. For all the light bulbs, the mean burn time is approximately 1248 hours and the standard deviation is approximately 84.1.