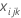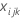Sum of squares (SS)
The sum of squares (SS) is the sum of squared distances, and is a measure of the variability that is from different sources.
- SSPart
-

- SSOperator
-

- SSPart*Operator
-
SSPart*Operator = SSTotal – (SSPart + SSOperator + SSRepeatability)
- SSRepeatability
- When the interaction term is in the ANOVA table, use the following
formula for the sum of squares for repeatability:

- SSTotal
-
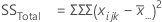
Degrees of freedom (DF)
The degrees of freedom (DF) for each SS (sums of squares). In general, DF measures how much information is available to calculate each SS.
- DFPart
-

- DFOperator
-
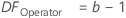
- DFPart*Operator
-

- DFRepeatability
-

- DFTotal
-
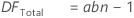
Mean squares (MS)
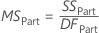
The mean squares (MS) is the variability in the data from different sources. MS accounts for the fact that different sources have different numbers of levels or possible values.
- MSPart
-
- MSOperator
-

- MSPart*Operator
-
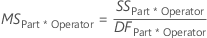
- MSRepeatability
-

F
The F-statistic is used to determine whether the effects of Operator, Part, or Operator*Part are statistically significant.
- FPart
-
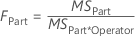
- FOperator
-
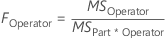
- FPart*Operator
-
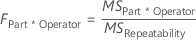
p-value
The p-value is the probability of obtaining a test statistic (such as the F-statistic) that is at least as extreme as the value that is calculated from the sample, if the null hypothesis is true.