In This Topic
Step 1: Determine whether your process is stable
Before you evaluate the capability of your process, determine whether it is stable. If your process is not stable, the estimates of process capability may not be reliable.
Use the P chart to visually monitor the %defective and to determine whether the %defective is stable and in control.
Red points indicate subgroups that fail at least one of the tests for special causes and are not in control. Out-of-control points indicate that the process may not be stable and that the results of a capability analysis may not be reliable. You should identify the cause of out-of-control points and eliminate special-cause variation before you analyze process capability.
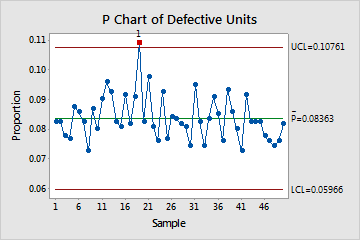
In this P chart, most of the points vary randomly and are within the control limits. No trends or patterns are present. However, the proportion of defective units for day 19 is out of control. Before you evaluate process capability, investigate and eliminate any special causes that may have contributed to the unusually high rate of defectives on that day.
Step 2: Determine whether the data follow a binomial distribution
Before you evaluate the capability of your process, determine whether it follows a binomial distribution. If your data do not follow a binomial distribution, the estimates of process capability may not be reliable. The graph that Minitab displays to evaluate the distribution of the data depends on whether your subgroup sizes are equal or unequal.
Subgroup sizes are equal
If your subgroup sizes are all the same, Minitab displays a binomial plot.
Examine the plot to determine whether the plotted points approximately follow a straight line. If not, then the assumption that the data were sampled from a binomial distribution may be false.
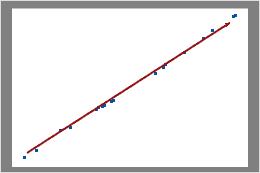
Binomial
In this plot, the data points fall closely along the line. You can assume that the data follow a binomial distribution.
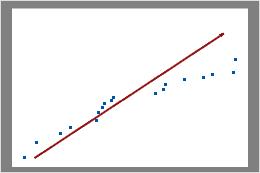
Not binomial
In this plot, the data points do not fall along the line near the top right. These data do not follow a binomial distribution and cannot be reliably evaluated using binomial capability analysis.
Subgroup sizes are not equal
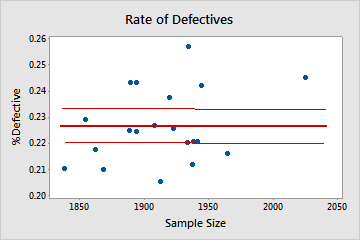
If the subgroup sizes vary, Minitab displays a rate of defectives plot.
Examine the plot to assess whether the %defective is randomly distributed across sample sizes or whether a pattern is present. If your data fall randomly about the center line, you conclude that the data follow a binomial distribution.
Binomial
In this plot, the points are scattered randomly around the center line. You can assume that the data follow a binomial distribution. Therefore, the data can be evaluated using binomial capability analysis.
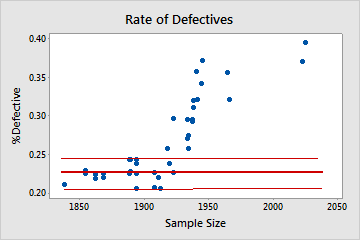
Not binomial
In this plot, the pattern is not random. For sample sizes that are greater than 1900, the %defective rate increases as the sample size increases. This result indicates a correlation between sample size and percentage of defectives. Therefore, the data do not follow a binomial distribution and cannot be reliably evaluated using binomial capability analysis.
Step 3: Evaluate the percentage of defective units
Examine the %defective estimate and CI
Use the mean %defective of the sample data to estimate the mean %defective for the process. Use the confidence interval as a margin of error for the estimate.
The confidence interval provides a range of likely values for the actual value of the %defective in your process (if you could collect and analyze all the items it produces). At a 95% confidence level, you can be 95% confident that the actual %defective of the process is contained within the confidence interval. That is, if you collect 100 random samples from your process, you can expect approximately 95 of the samples to produce intervals that contain the actual value of %defective.
The confidence interval helps you assess the practical significance of your sample estimate. If you have a maximum allowable %defective value that is based on process knowledge or industry standards, compare the upper confidence bound to this value. If the upper confidence bound is less than the maximum allowable %defective value, then you can be confident that your process meets specifications, even when taking into account variability from random sampling that affects the estimate.
| Summary Stats | |
|---|---|
| (95.0% confidence) | |
| %Defective: | 0.39 |
| Lower CI: | 0.24 |
| Upper CI: | 0.60 |
| Target: | 0.50 |
| PPM Def: | 3931 |
| Lower CI: | 2435 |
| Upper CI: | 6003 |
| Process Z: | 2.6579 |
| Lower CI: | 2.5120 |
| Upper CI: | 2.8155 |
Key Results: %Defective, CI
The results for binomial capability analysis include a Summary Stats table, located in the lower middle portion of the output. In this simulated Summary Stats table, the Target (0.50%) indicates the maximum allowable %defective for the process. The %defective estimate is 0.39%, which is below the maximum allowable %defective. However, the upper CI for %defective is 0.60%, which exceeds the maximum allowable value. Therefore, you cannot be 95% confident that the process is capable. You may need to use a larger sample size, or reduce the variability of the process, to obtain a narrower confidence interval for the %defective estimate.
Determine whether you have enough data for a reliable estimate
Use the Cumulative %Defective plot to determine whether you have enough samples for a stable estimate of the %defective.
Examine the %defective for the time-ordered samples to see how the estimate changes as you collect more samples. Ideally, the %defective stabilizes after several samples, as shown by a flattening of the plotted points along the mean %defective line.
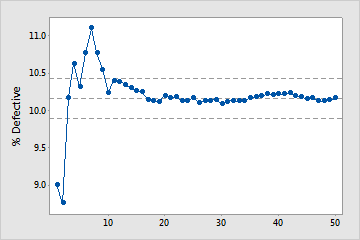
Enough samples
In this plot, the %defective stabilizes along the mean %defective line. Therefore, the capability study includes enough samples to produce a stable, reliable estimate of the mean %defective.
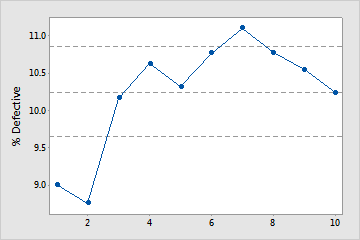
Not enough samples
In this plot, the %defective does not stabilize. Therefore, the capability study does not include enough samples to reliably estimate the mean %defective.
