In This Topic
S
S represents the standard deviation of the distance between the data values and the fitted values. S is measured in the units of the response.
Interpretation
Use S to assess how well the model describes the response. S is measured in the units of the response variable and represents how far the data values fall from the fitted values. The lower the value of S, the better the model describes the response. However, a low S value by itself does not indicate that the model meets the model assumptions. You should check the residual plots to verify the assumptions.
For example, you work for a potato chip company that examines the factors that affect the percentage of crumbled potato chips per container. You reduce the model to the significant predictors, and S is calculated as 1.79. This result indicates that the standard deviation of the data points around the fitted values is 1.79. If you are comparing models, values that are lower than 1.79 indicate a better fit, and higher values indicate a worse fit.
R-sq
R2 is the percentage of variation in the response that is explained by the model. It is calculated as 1 minus the ratio of the error sum of squares (which is the variation that is not explained by model) to the total sum of squares (which is the total variation in the model).
Interpretation
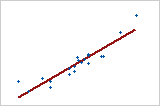
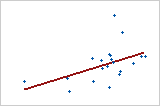
Use R2 to determine how well the model fits your data. The higher the R2 value, the better the model fits your data. R2 is always between 0% and 100%.
-
R2 always increases when you add additional predictors to a model. For example, the best five-predictor model will always have an R2 that is at least as high as the best four-predictor model. Therefore, R2 is most useful when you compare models of the same size.
-
Small samples do not provide a precise estimate of the strength of the relationship between the response and predictors. For example, if you need R2 to be more precise, you should use a larger sample (typically, 40 or more).
-
Goodness-of-fit statistics are just one measure of how well the model fits the data. Even when a model has a desirable value, you should check the residual plots to verify that the model meets the model assumptions.
R-sq (adj)
Adjusted R2 is the percentage of the variation in the response that is explained by the model, adjusted for the number of predictors in the model relative to the number of observations. Adjusted R2 is calculated as 1 minus the ratio of the mean square error (MSE) to the mean square total (MS Total).
Interpretation
Use adjusted R2 when you want to compare models that have different numbers of predictors. R2 always increases when you add a predictor to the model, even when there is no real improvement to the model. The adjusted R2 value incorporates the number of predictors in the model to help you choose the correct model.
| Model | % Potato | Cooling rate | Cooking temp | R2 | Adjusted R2 |
|---|---|---|---|---|---|
| 1 | X | 52% | 51% | ||
| 2 | X | X | 63% | 62% | |
| 3 | X | X | X | 65% | 62% |
The first model yields an R2 of more than 50%. The second model adds cooling rate to the model. Adjusted R2 increases, which indicates that cooling rate improves the model. The third model, which adds cooking temperature, increases the R2 but not the adjusted R2. These results indicate that cooking temperature does not improve the model. Based on these results, you consider removing cooking temperature from the model.
PRESS
The prediction error sum of squares (PRESS) is a measure of the deviation between the fitted values and the observed values. PRESS is similar to the sum of squares of the residual error (SSE), which is the summation of the squared residuals. However, PRESS uses a different calculation for the residuals. The formula used to calculate PRESS is equivalent to a process of systematically removing each observation from the data set, estimating the regression equation, and determining how well the model predicts the removed observation.
Interpretation
Use PRESS to assess your model's predictive ability. Usually, the smaller the PRESS value, the better the model's predictive ability. Minitab uses PRESS to calculate the predicted R2, which is usually more intuitive to interpret. Together, these statistics can prevent over-fitting the model. An over-fit model occurs when you add terms for effects that are not important in the population, although they may appear important in the sample data. The model becomes tailored to the sample data and therefore, may not be useful for making predictions about the population.
R-sq (pred)
Predicted R2 is calculated with a formula that is equivalent to systematically removing each observation from the data set, estimating the regression equation, and determining how well the model predicts the removed observation. The value of predicted R2 ranges between 0% and 100%. (While the calculations for predicted R2 can produce negative values, Minitab displays zero for these cases.)
Interpretation
Use predicted R2 to determine how well your model predicts the response for new observations. Models that have larger predicted R2 values have better predictive ability.
A predicted R2 that is substantially less than R2 may indicate that the model is over-fit. An over-fit model occurs when you add terms for effects that are not important in the population. The model becomes tailored to the sample data and, therefore, may not be useful for making predictions about the population.
Predicted R2 can also be more useful than adjusted R2 for comparing models because it is calculated with observations that are not included in the model calculation.
For example, an analyst at a financial consulting company develops a model to predict future market conditions. The model looks promising because it has an R2 of 87%. However, the predicted R2 is 52%, which indicates that the model may be over-fit.
AICc and BIC
The corrected Akaike’s Information Criterion (AICc) and the Bayesian Information Criterion (BIC) are measures of the relative quality of a model that account for fit and the number of terms in the model.
Interpretation
Use AICc and BIC to compare different models. Smaller values are desirable. However, the model with the least value for a set of predictors does not necessarily fit the data well. Also use tests and residual plots to assess how well the model fits the data.
Both AICc and BIC assess the likelihood of the model and then apply a penalty for adding terms to the model. The penalty reduces the tendency to overfit the model to the sample data. This reduction can yield a model that performs better in general.
As a general guideline, when the number of parameters is small relative to the sample size, BIC has a larger penalty for the addition of each parameter than AICc. In these cases, the model that minimizes BIC tends to be smaller than the model that minimizes AICc.
In some common cases, such as screening designs, the number of parameters is usually large relative to the sample size. In these cases, the model that minimizes AICc tends to be smaller than the model that minimizes BIC. For example, for a 13-run definitive screening design, the model that minimizes AICc will tend to be smaller than the model that minimizes BIC among the set of models with 6 or more parameters.
For more information on AICc and BIC, see Burnham and Anderson.1
Test S
Interpretation
Use test S to assess the performance of the model on new data. The lower the value of test S, the closer the predictions of the model are to the actual values in the test data set.
An S value that is substantially less than the test S value may indicate that the model is over-fit. An over-fit model occurs when you add terms for effects that are not important in the population. The model becomes tailored to the sample data and, therefore, may not be useful for making predictions about the population.
For example, you work for a potato chip company that examines the factors that affect the percentage of crumbled chips per container. You reduce the model to the significant predictors and find that S is 1.79, but test S is 17.63. Because the test S is very different from the S from the training set, you decide that the test S gives a better indication of how the model will perform for new data.
A low test S value by itself does not indicate that the model meets the model assumptions. You should check the residual plots to verify the assumptions.
Test R-sq
Interpretation
Use test R2 to determine how well your model fits new data. Models that have larger test R2 values tend to perform better on new data. You can use test R2 to compare the performance of different models.
A test R2 that is substantially less than R2 may indicate that the model is over-fit. An over-fit model occurs when you add terms for effects that are not important in the population. The model becomes tailored to the training data and, therefore, may not be useful for making predictions about the population.
For example, an analyst at a financial consulting company develops a model to predict future market conditions. The model looks promising because it has an R2 of 87%. However, the test R2 is 52%, which indicates that the model may be over-fit.
A high test R2 value by itself does not indicate that the model meets the model assumptions. You should check the residual plots to verify the assumptions.
K-fold S
Interpretation
Use K-fold S to assess the performance of the model on new data. The lower the value of K-fold S, the closer the predictions of the model are to the actual values in the fold when the data in the fold are not part of the estimation of the model.
An S value that is substantially less than the K-fold S value may indicate that the model is over-fit. An over-fit model occurs when you add terms for effects that are not important in the population. The model becomes tailored to the sample data and, therefore, may not be useful for making predictions about the population.
For example, you work for a potato chip company that examines the factors that affect the percentage of crumbled chips per container. You reduce the model to the significant predictors and find that S is 1.79, but K-fold S is 17.63. Because the K-fold S is very different from the S from the training set, you decide that the K-fold S gives a better indication of how the model will perform for new data.
A low K-fold S value by itself does not indicate that the model meets the model assumptions. You should check the residual plots to verify the assumptions.
K-fold R-sq
Interpretation
Use K-fold R2 to determine how well your model fits new data. Models that have larger K-fold R2 values tend to perform better on new data. You can use K-fold R2 to compare the performance of different models.
A K-fold R2 that is substantially less than R2 may indicate that the model is over-fit. An over-fit model occurs when you add terms for effects that are not important in the population. The model becomes tailored to the training data and, therefore, may not be useful for making predictions about the population.
For example, an analyst at a financial consulting company develops a model to predict future market conditions. The model looks promising because it has an R2 of 87%. However, the K-fold R2 is 52%, which indicates that the model may be over-fit.
A high K-fold R2 value by itself does not indicate that the model meets the model assumptions. You should check the residual plots to verify the assumptions.
K-fold stepwise R-sq
Interpretation
Use k-fold stepwise R2 to determine the number of terms in a model. Minitab calculates k-fold stepwise R-sq when you perform forward selection with validation with k-fold cross validation. K-fold stepwise R2 results from separate forward selections for each fold. Minitab uses the k-fold stepwise R2 to determine the best step in forward selection. Once forward selection is complete for each fold, Minitab performs forward selection on the full data set. With the full dataset, Minitab produces regression results for the model at the best step according to the k-fold stepwise R2 criterion.
To evaluate the predictive performance of a model with k-fold cross validation, use the k-fold R2 statistic instead.
Mallows' Cp
Mallows' Cp can help you choose between competing multiple regression models. Mallows' Cp compares the full model to models with the subsets of predictors. It helps you strike an important balance with the number of predictors in the model. A model with too many predictors can be relatively imprecise while a model with too few predictors can produce biased estimates. Using Mallows' Cp to compare regression models is only valid when you start with the same complete set of predictors.
Interpretation
A Mallows' Cp value that is close to the number of predictors plus the constant indicates that the model produces relatively precise and unbiased estimates.
A Mallows' Cp value that is greater than the number of predictors plus the constant indicates that the model is biased and does not fit the data well.
