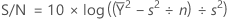In Taguchi designs, a measure of robustness used to identify control factors that reduce variability in a product or process by minimizing the effects of uncontrollable factors (noise factors). Control factors are those design and process parameters that can be controlled. Noise factors cannot be controlled during production or product use, but can be controlled during experimentation. In a Taguchi designed experiment, you manipulate noise factors to force variability to occur and from the results, identify optimal control factor settings that make the process or product robust, or resistant to variation from the noise factors. Higher values of the signal-to-noise ratio (S/N) identify control factor settings that minimize the effects of the noise factors.
Taguchi experiments often use a 2-step optimization process. In step 1 use the signal-to-noise ratio to identify those control factors that reduce variability. In step 2, identify control factors that move the mean to target and have a small or no effect on the signal-to-noise ratio.
| Signal-to-noise ratio | Goal of the experiment | Data characteristics | Signal-to-noise ratio formulas |
|---|---|---|---|
| Larger is better | Maximize the response | Positive | S/N = −10 *log(Σ(1/Y2)/n) |
| Nominal is best | Target the response and you want to base the signal-to-noise ratio on standard deviations only | Positive, zero, or negative | S/N = −10 *log(σ2) |
| Nominal is best (default) | Target the response and you want to base the signal-to-noise ratio on means and standard deviations | Non-negative with an "absolute zero" in which the standard deviation is zero when the mean is zero |
The adjusted formula is:
|
| Smaller is better | Minimize the response | Non-negative with a target value of zero | S/N = −10 *log(Σ(Y2)/n)) |
For Taguchi dynamic designs, Minitab provides one signal-to-noise ratio (and an adjusted formula), which is closely related to the nominal-is-best S/N ratio for static designs.
Note
The Nominal is Best (default) signal-to-noise ratio is useful for analyzing or identifying scaling factors, which are factors in which the mean and standard deviation vary proportionally. Scaling factors can be used to adjust the mean on target without affecting signal-to-noise ratios.