What is a response surface design?
A response surface design is a set of advanced design of experiments (DOE) techniques that help you better understand and optimize your response. Response surface design methodology is often used to refine models after you have determined important factors using screening designs or factorial designs; especially if you suspect curvature in the response surface.
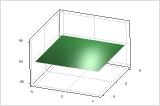
Response surface with no curvature

Response surface with curvature
- Understanding or mapping a region of a response surface. Response surface equations model how changes in variables affect a response of interest.
- Finding the levels of variables that optimize a response.
- Selecting the operating conditions to meet specifications.
For example, you would like to determine the best conditions for injection-molding a plastic part. You first used a screening or factorial experiment to determine the significant factors (temperature, pressure, cooling rate). You can use a response surface designed experiment to determine the optimal settings for each factor.
- Central Composite designs
- Central Composite designs can fit a full quadratic model. They are often used when the design plan calls for sequential experimentation because these designs can include information from a correctly planned factorial experiment.
- Box-Behnken designs
- Box-Behnken designs usually have fewer design points than central composite designs, thus, they are less expensive to run with the same number of factors. They can efficiently estimate the first- and second-order coefficients; however, they can't include runs from a factorial experiment. Box-Behnken designs always have 3 levels per factor, unlike central composite designs which can have up to 5. Also unlike central composite designs, Box-Behnken designs never include runs where all factors are at their extreme setting, such as all of the low settings.
What is a central composite design
- Efficiently estimate first- and second-order terms.
- Model a response variable with curvature by adding center and axial points to a previously-done factorial design.
Central composite designs are especially useful in sequential experiments because you can often build on previous factorial experiments by adding axial and center points.
For example, you would like to determine the best conditions for injection-molding a plastic part. You first run a factorial experiment and determine the significant factors: temperature (levels set at 190° and 210°) and pressure (levels set at 50MPa and 100MPa). If the factorial design detects curvature, you can use a response surface designed experiment to determine the optimal settings for each factor. The design points for this experiment are below.
| 210°, 50MPa | 214.1°, 75MPa (axial point) | 210°, 100MPa |
| 200°, 39.6MPa (axial point) | 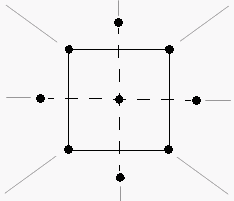 |
200°, 110.4MPa (axial point) |
| 190°, 50MPa | 185.9°, 75MPa (axial point) | 190°, 100MPa |
- Orthogonal blocks
- Often, central composite designs are done in more than one block. Central composite designs can create orthogonal blocks, letting model terms and block effects be estimated independently and minimizing the variation in the regression coefficients.
- Rotatability
- Rotatable designs provide constant prediction variance at all points that are equidistant from the design center.
What is a face-centered design?
Face centered designs are a type of central composite design with an alpha of 1. In this design the axial points are at the center of each face of the factorial space, so levels = + 1. This variety of design requires 3 levels of each factor. Augmenting an existing factorial or resolution V design with appropriate axial points can also produce this design.
What is a Box-Behnken design?
A Box-Behnken design is a type of response surface design that does not contain an embedded factorial or fractional factorial design.
- Temperature: 190° and 210°
- Pressure: 50Mpa and 100Mpa
- Injection speed: 10 mm/s and 50 mm/s
- Temperature: 190°, 200°, and 210°
- Pressure: 50Mpa, 75Mpa, and 100Mpa
- Injection speed: 10 mm/s, 30 mm/s, and 50 mm/s
Box-Behnken designs have treatment combinations that are at the midpoints of the edges of the experimental space and require at least three continuous factors. The following figure shows a three-factor Box-Behnken design. Points on the diagram represent the experimental runs that are done:
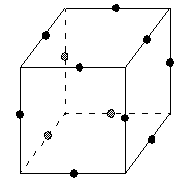
These designs allow efficient estimation of the first- and second-order coefficients. Because Box-Behnken designs often have fewer design points, they can be less expensive to do than central composite designs with the same number of factors. However, because they do not have an embedded factorial design, they are not suited for sequential experiments.
Box-Behnken designs can also prove useful if you know the safe operating zone for your process. Central composite designs usually have axial points outside the "cube." These points may not be in the region of interest, or may be impossible to conduct because they are beyond safe operating limits. Box-Behnken designs do not have axial points, thus, you can be sure that all design points fall within your safe operating zone. Box-Behnken designs also ensure that all factors are not set at their high levels at the same time.
