What is a factorial design?
A factorial design is type of designed experiment that lets you study of the effects that several factors can have on a response. When conducting an experiment, varying the levels of all factors at the same time instead of one at a time lets you study the interactions between the factors.
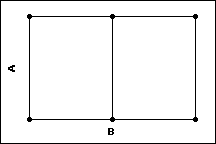
Two Factor Design
- 2 levels of factor A
- 3 levels of factor B
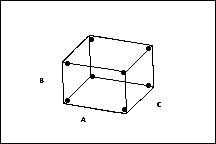
Three Factor Design
2 levels of each factor
You can either run the full factorial design or a fraction of the factorial design.
Note
When you have a factorial design with center points you can test whether there is curvature in the response surface. However, you cannot model the effect of that curvature anywhere but at the center point. In other words, you can only calculate the fitted values at the corner points and the center point of the design, and thus cannot create a contour plot. You need to have quadratic terms (for example, square terms) in the model in order to model the curvature across the whole response surface. This is possible with a response surface design. You can augment the factorial design with axial points to create a central composite response surface design from a factorial design.
What is a full factorial and fractional factorial design?
Full factorial designs
A full factorial design is a design in which researchers measure responses at all combinations of the factor levels. Minitab offers two types of full factorial designs:
- 2-level full factorial designs that contain only 2-level factors.
- general full factorial designs that contain factors with more than two levels.
The number of runs necessary for a 2-level full factorial design is 2k where k is the number of factors. As the number of factors in a 2-level factorial design increases, the number of runs necessary to do a full factorial design increases quickly. For example, a 2-level full factorial design with 6 factors requires 64 runs; a design with 9 factors requires 512 runs. A half-fraction, fractional factorial design would require only half of those runs.
Fractional factorial designs
A fractional design is a design in which experimenters conduct only a selected subset or "fraction" of the runs in the full factorial design. Fractional factorial designs are a good choice when resources are limited or the number of factors in the design is large because they use fewer runs than the full factorial designs.
A fractional factorial design uses a subset of a full factorial design, so some of the main effects and 2-way interactions are confounded and cannot be separated from the effects of other higher-order interactions. Usually experimenters are willing to assume the higher-order effects are negligible in order to achieve information about main effects and low-order interactions with fewer runs.
What is a 2-level full factorial design?
In a 2-level full factorial design, each experimental factor has only two levels. The experimental runs include all combinations of these factor levels. Although 2-level factorial designs are unable to explore fully a wide region in the factor space, they provide useful information for relatively few runs per factor. Because 2-level factorial designs can identify major trends, you can use them to provide direction for additional experimentation. For example, when you need to explore a region where you believe optimal settings may exist, you can augment a factorial design to form a central composite design.
Comparison
The following diagrams show a full factorial design versus a ½ fractional factorial design.
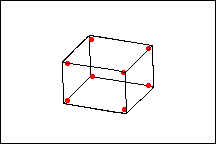
Full factorial design
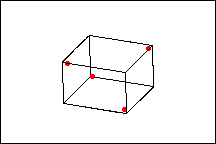
½ Fraction factorial design
The full factorial design contains twice as many design points as the ½ fraction design. The response is only measured at four of the possible eight corner points of the factorial portion of the design. However, with this design, the main effects will be confounded with the 2-way interactions.
How Minitab orders the fractions of a design
| Fraction | Standard (Yates) Order | Design Generator |
|---|---|---|
| 1 | – – – | D = –AB, E = –AC, F = –BC |
| 2 | + – – | D = +AB, E = –AC, F = –BC |
| 3 | – + – | D = –AB, E = +AC, F = –BC |
| 4 | + + – | D = +AB, E = +AC, F = –BC |
| 5 | – – + | D = –AB, E = –AC, F = +BC |
| 6 | + – + | D = +AB, E = –AC, F = +BC |
| 7 | – + + | D = –AB, E = +AC, F = +BC |
| 8 | + + + | D = +AB, E = +AC, F = +BC |
The principal fraction is always the last one, the one that has all + signs.
| Run | A | B | C | D = AB | E = –AC | F = –BC |
|---|---|---|---|---|---|---|
| 1 | – | – | – | + | – | – |
| 2 | + | – | – | – | + | – |
| 3 | – | + | – | – | – | + |
| 4 | + | + | – | + | + | + |
| 5 | – | – | + | + | + | + |
| 6 | + | – | + | – | – | + |
| 7 | – | + | + | – | + | – |
| 8 | + | + | + | + | – | – |
Choosing a fraction other than the default
When you create a fractional factorial design, Minitab uses the principal fraction by default. The principal fraction is the fraction where all signs are positive. However, there may be situations when a design contains points that are impractical to conduct and choosing an appropriate fraction can avoid these points.
- D = –AB E = –AC
- D = AB E = –AC
- D = –AB E = AC
- D = AB E = AC
For example, suppose you could not conduct your design with all five factors set at their high level. The principal fraction contains this point, but the third fraction does not.
