Enter your data
In Variable, enter a column of numeric data that were collected at regular intervals and recorded in time order. If your data are in multiple columns (for example, you have data for each year in a separate column), you must stack the data into a single column.
In this worksheet, Sales contains the number of computers that are sold each month.
| C1 |
|---|
| Sales |
| 195000 |
| 213330 |
| 208005 |
| 249000 |
| 237040 |
Weight to Use in Smoothing
The weights adjust the amount of smoothing by defining how each component reacts to current conditions. Usually, you want to smooth the data enough to reduce the noise (irregular fluctuations) so that the pattern is more apparent. However, don't smooth the data so much that you lose important details.
If you do not know a good weight, select Optimal ARIMA. Then, you can increase or decrease the weight after you examine the time series plot. Lower weights produce a smoother line, and higher weights produce a less smooth line. Use smaller weights for noisy data so that the smoothed values don't fluctuate with the noise.
- Optimal ARIMA
- Minitab uses the weight that minimizes the sum of the squared residuals in an ARIMA (0,1,1) model. An ARIMA (0,1,1) model calculates the differences of the data and includes a moving average term of order 1.
- Use
- Usually, a weight between 0 and 1 works well. Use smaller weights for noisy data so that the smoothed values don't fluctuate with the noise. Lower weights give less weight to recent data, which produces a smoother line. Higher weights give more weight to recent data, which produces a less smooth line. To calculate naive forecasts, use a weight of 1. For more information on naive forecasting, go to Forecasting with time series analysis and click "What is naive forecasting?".
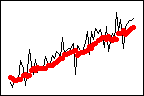
Weight = 0.2
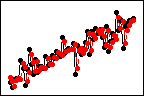
Weight = 0.8
Generate forecasts
Complete the following steps to generate forecasts for your time series.
- Select Generate forecasts.
- In Number of forecasts, enter the number of consecutive time periods that you want forecasts for.
- In Starting from
origin, specify the row number for the first forecast. If you leave this field blank, Minitab starts the forecasts at the end of the time series.
If you enter a value, Minitab uses only the data up to that row number for the forecasts. The forecast values differ from the fits because Minitab uses all of the data to calculate the fits.
For example, an analyst has monthly data for January through December. In December, the analyst wants to generate a forecast for the next month, but December's data are incomplete. In Number of forecasts, the analyst enters 2. In Starting from origin, the analyst enters 12. Minitab uses the data through November to generate forecasts for December and January.
