In This Topic
GLM model
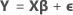
Notation
| Term | Description |
|---|---|
| Y | vector of responses |
| X | design matrix |
| β | vector of parameters |
| ε | vector of independent normal random variables |
Design matrix
General Linear Model uses a regression approach to fit the model that you specify. First Minitab creates a design matrix, from the factors and covariates, and the model that you specify. The columns of this matrix are the predictors for the regression.
The design matrix has n rows, where n = number of observations and several blocks of columns, corresponding to the terms in the model. The first block is for the constant and contains just one column, a column of all ones. The block for a covariate also contains just one column, the covariate column itself. The block of columns for a factor contains r columns, where r = degrees of freedom for the factor, and they are coded as shown in the example below.
Suppose A is a factor with 4 levels. Then it has 3 degrees of freedom and its block contains 3 columns, call them A1, A2, A3.
| Level of A | A1 | A2 | A3 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
| 4 | –1 | –1 | –1 |
Suppose factor B has 3 levels nested within each level of A. Then its block contains (3 - 1) x 4 = 8 columns, call them B11, B12, B21, B22, B31, B32, B41, B42, coded as follows:
| Level of A | Level of B | B11 | B12 | B21 | B22 | B31 | B32 | B41 | B42 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 3 | –1 | –1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 2 | 3 | 0 | 0 | –1 | –1 | 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 3 | 2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 3 | 3 | 0 | 0 | 0 | 0 | –1 | –1 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 4 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | –1 | –1 |
To calculate the columns for an interaction term, just multiply all the corresponding columns for the factors and/or covariates in the interaction. For example, suppose factor A has 6 levels, C has 3 levels, D has 4 levels, and Z and W are covariates. Then the term A * C * D * Z * W * W has 5 x 2 x 3 x 1 x 1 x 1 = 30 columns. To obtain them, multiply each column for A by each for C, by each for D, by the covariates Z once and W twice.
Box-Cox transformation
Box-Cox transformation selects lambda values, as shown below, which minimize the residual sum of squares. The resulting transformation is Y λ when λ ≠ 0 and ln(Y) when λ = 0. When λ < 0, Minitab also multiplies the transformed response by −1 to maintain the order from the untransformed response.
Minitab searches for an optimal value between −2 and 2. Values that fall outside of this interval might not result in a better fit.
Here are some common transformations where Y′ is the transform of the data Y:
| Lambda (λ) value | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 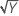 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
Weighted regression
Weighted least squares regression is a method for dealing with observations that have nonconstant variances. If the variances are not constant, observations with:
- large variances should be given relatively small weights
- small variances should be given relatively large weights
The usual choice of weights is the inverse of pure error variance in the response.
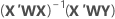

Notation
| Term | Description |
|---|---|
| X | design matrix |
| X' | transpose of the design matrix |
| W | an n x n matrix with the weights on the diagonal |
| Y | vector of response values |
| n | number of observations |
| wi | weight for the ith observation |
| yi | response value for the ith observation |
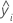 | fitted value for the ith observation |
How Minitab removes highly correlated predictors from the regression equation in Fit General Linear Model
- Minitab performs a QR decomposition on the X-matrix.
Note
Using the QR decomposition to calculate R2 is quicker than using least-squares regression.
- Minitab regresses a predictor on all other predictors and calculates the R2 value. If 1 – R2 < 4 * 2.22e-16, then the predictor fails the test and is removed from the model.
- Minitab repeats steps 1 and 2 for the remaining predictors.
Example
- Minitab regresses X5 on X1-X4. If 1 – R2 is greater than 4 * 2.22e-16 then X5 remains in the equation. X5 passes the test and remains in the equation.
- Minitab regresses X4 on X1, X2, X3, and X5. Suppose 1 – R2 for this regression is greater than 4 * 2.22e-16 and thus remains in the equation.
- Minitab regresses X3 on X1, X2, X4, and X5 and calculates the R2 value. X3 fails the test and is removed from the equation.
- Minitab performs a new QR decomposition on the X-matrix and regresses X2 on the remaining predictors, X1, X4, and X5. X2 passes the test.
- Minitab regresses X1 on X2, X4, and X5. It fails the test and is removed from the equation.
Minitab regresses Y on X2, X4, X5. The results include a message saying that predictors X1 and X3 cannot be estimated and were removed from the model.
Note
You can use the TOLERANCE subcommand with the GLM session command to force Minitab to keep a predictor in the model that is highly correlated with a different predictor. However, lowering the tolerance can be dangerous, possibly producing numerically inaccurate results.
