Herunterladen des Makros
Vergewissern Sie sich, dass Sie in Minitab den Speicherort des heruntergeladenen Makros angegeben haben. Wählen Sie aus. Navigieren Sie im Feld Speicherort für Makros zu dem Speicherort, an dem Sie Makrodateien ablegen.
Wichtig
Wenn Sie einen älteren Webbrowser verwenden und auf die Schaltfläche Herunterladen klicken, wird die Datei möglicherweise in Quicktime geöffnet; für dieses Programm wird dieselbe Dateinamenerweiterung „.mac“ wie für Minitab-Makros verwendet. Um das Makro zu speichern, klicken Sie mit der rechten Maustaste auf die Schaltfläche Herunterladen, und wählen Sie Ziel speichern unter aus.
Erforderliche Eingaben
Sie benötigen eine Spalte mit Zeitreihendaten.
Optionale Eingaben
- AR K…K
- Wenn geschätzte autoregressive Parameter vorliegen und das Spektralmodell geprüft werden soll, geben Sie diese Parameter hier ein.
- DIF K
- Wenn eine Differenzbildungskomponente vorliegt, geben Sie die Ordnung der Differenzbildung hier ein.
- MA K…K
- Wenn geschätzte Parameter für einen gleitenden Durchschnitt vorliegen und das Spektralmodell geprüft werden soll, geben Sie diese Parameter hier ein.
- VARIANCE K
- Geben Sie die geschätzte Varianz ein (Standardwert = 1,0).
- SMOOTH K
- Geben Sie die Länge des gleitenden Durchschnitts ein (Standardwert = 3). Die Länge des gleitenden Durchschnitts muss eine ungerade ganze Zahl sein.
- ONEDOC
- Geben Sie dies an, wenn alle Grafiken auf einer Seite angezeigt werden sollen.
- SPERIOD C C
- Geben Sie dies an, wenn die Koordinaten für das Periodogramm gespeichert werden sollen. Die erste Spalte enthält I(Omega) und die zweite Spalte Omega.
- SCUMUL C C C C
- Geben Sie dies an, wenn die Koordinaten für das kumulative Periodogramm gespeichert werden sollen. Die erste Spalte enthält U(j), die zweite Spalte die obere Signifikanzgrenze, die dritte Spalte die untere Signifikanzgrenze und die vierte Spalte die x-Achse.
- SSPEC C C C C
- Geben Sie dies an, wenn die Koordinaten für die Spektralschätzung gespeichert werden sollen. Die erste Spalte enthält die Spektralschätzung, die zweite Spalte die obere Konfidenzgrenze, die dritte Spalte die untere Konfidenzgrenze und die vierte Spalte Omega.
- SMODEL C C C C
- Geben Sie dies an, wenn die Koordinaten für die Prüfung des Spektralmodells gespeichert werden sollen. Die erste Spalte enthält F(Omega), die zweite Spalte die obere Konfidenzgrenze, die dritte Spalte die untere Konfidenzgrenze, die vierte Spalte die Spektralschätzungen und die fünfte Spalte Omega.
Ausführen des Makros
Angenommen, die Daten sind in C1 gespeichert. Um das Makro auszuführen, wählen Sie aus, und geben Sie Folgendes ein:
%SPECTRAL C1Klicken Sie auf Durchlauf.
Weitere Informationen
Periodogramm
Das Periodogramm ist ein Werkzeug, mit dem zyklische Komponenten in einer Zeitreihe erkannt werden können. Das Periodogramm ist folgendermaßen definiert:
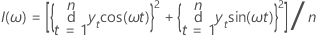
Obwohl das Periodogramm für ω = 0 definiert ist, wird dieser Punkt ausgeschlossen, da er dem Stichprobenmittelwert entspricht (der belanglos ist). Wenn n ungerade ist, wird ω = π ausgeschlossen.
Kumulatives Periodogramm
Das kumulative Periodogramm ist eine direkte Anwendung des Periodogramms zum Testen der Hypothese, dass eine bestimmte Zeitreihe Zufallsrauschen darstellt. Das kumulative Periodogramm ist ein effektives Bewertungswerkzeug für Residuen. Das kumulative Periodogramm ist folgendermaßen definiert:
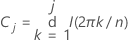
j=1, ..., m, wobei m die größte ganze Zahl streng kleiner als n/2 ist.
Ein Diagramm von U j im Vergleich zu j /(m −1) wird als kumulatives Periodogramm bezeichnet.
Außerdem können für den Test der Hypothese, dass Zufallsrauschen vorliegt, kritische Werte festgelegt werden. Das Makro verwendet ein Signifikanzniveau von 10 % (kritischer Wert = 1,224). Die kritische Region wird durch zwei parallele Linien mit dem folgenden Schnittpunkt mit der y-Achse definiert:
Spektralschätzung
Die Spektralschätzung,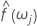 
, kann einfach durch Berechnen eines gleitenden Durchschnitts der Ordnung 2p+1 (wobei p eine positive ganze Zahl ist) der durch das Periodogramm berechneten Ordinaten abgeleitet werden. Außerdem können Konfidenzgrenzen für diese Spektralschätzung festgelegt werden:
Die obere und untere Konfidenzgrenze können definiert werden als:
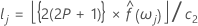
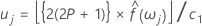
Spektrum eines ARMA-Prozesses
Die Spektralschätzung ist die Schätzung des Spektrums auf der Grundlage der Daten. Das Spektrum basiert auf den tatsächlichen Werten der Grundgesamtheit für die Modellparameter. Das Spektrum eines AR(p)-Prozesses kann folgendermaßen definiert werden:
Das Spektrum eines MA(q)-Prozesses kann folgendermaßen definiert werden:
Das Spektrum eines ARMA (p, q)-Prozesses (wobei p und q Ordnungen sind) kann folgendermaßen definiert werden:
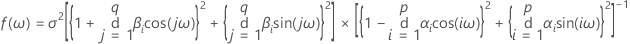
Prüfung des Spektralmodells für einen ARIMA-Prozess
Die aus einer beobachteten Zeitreihe berechnete Spektralschätzung kann mit dem tatsächlichen Spektrum auf der Grundlage der Modellparameter verglichen werden. Intuitiv lässt sich sagen: Wenn die Spektralschätzung ungefähr statistisch gleich dem tatsächlichen Spektrum ist, kann gefolgert werden, dass die Modellparameter angemessen für die Modellierung der Zeitreihe sind.
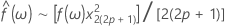
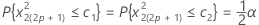
Daher können Konfidenzgrenzen festgelegt werden, um zu ermitteln, ob die Spektralschätzung innerhalb dieser Grenzen liegt.
Beispiel 1
Für ein Beispiel eines Periodogramms, eines kumulativen Periodogramms und einer Spektralschätzung betrachten Sie den Datensatz „Cycle 1, late follicular phase“ (Diggle, S. 228). Um das Makro auszuführen, wählen Sie aus, und geben Sie Folgendes ein:
%SPECTRAL C1Erstens weist das Periodogramm (nicht gezeigt) darauf hin, dass diese Zeitreihe aufgrund ihrer dominanten Spitze keine zyklische Komponente aufweist. Gelegentlich wird die x-Achse in eine aussagekräftigere Skala transformiert, so dass leichter ermittelt werden kann, an welchem Zeitpunkt die zyklische Komponente auftritt. Daher bietet das Makro Speicheroptionen, damit der Benutzer die Achse transformieren kann (anschließend können Sie mit den Grafikfunktionen in Minitab Diagramme generieren). Zweitens weist das kumulative Periodogramm darauf hin, dass diese Zeitreihe kein weißes Rauschen darstellt, weil einige der Datenpunkte jenseits der Signifikanzgrenzen liegen (dargestellt durch die parallelen gepunkteten Linien). Schließlich werden die Spektralschätzung (berechnet durch den standardmäßigen gleitenden Durchschnitt mit 3 Punkten) durch die rote Linie und die Konfidenzgrenzen durch die gepunkteten Linien dargestellt. Dieses Diagramm vermittelt eine ungefähre Idee des echten Spektrums der Grundgesamtheit. Alle drei Diagramme entsprechen den Diagrammen in Diggle (S. 52, 55, 106).
Beispiel 2
Für eine vollständige ARIMA-Analyse betrachten Sie den Datensatz „Cycle 2, early follicular phase“ (Diggle, S. 228). Zunächst werden das Periodogramm, das kumulative Periodogramm und die Spektralschätzung berechnet. Mit dem Unterbefehl ONEDOC werden diese drei Diagramme auf einer Seite angeordnet. Wählen Sie aus, und geben Sie Folgendes ein:
%SPECTRAL C2;
ONEDOC.
Die Grafiken (nicht gezeigt) verdeutlichen, dass diese Zeitreihe kein Zufallsrauschen ist, da sowohl das Periodogramm als auch die Spektralschätzung aufgrund der dominanten Spitzen bei kleinen Werten von Omega auf eine Zeitreihe mit niedriger Frequenz hinweisen und im kumulativen Periodogramm signifikante Punkte angezeigt werden. Daher wird Minitab verwendet, um diese Zeitreihe unter Verwendung des ARIMA-Algorithmus zu modellieren. Nach der Untersuchung von verschiedenen Modellen stellt sich ein AR(1)-Modell als das beste heraus.
Nun wird das Makro verwendet, um dieses empirische Modell auszuwerten. Beachten Sie, wie die Schätzung des autoregressiven Parameters und die Schätzung der Varianz (aus der ARIMA-Ausgabe) im nachfolgenden Befehl eingegeben werden. Wählen Sie aus, und geben Sie Folgendes ein:
%SPECTRAL C2;
AR 0.5860;
VARIANCE 0.20603;
ONEDOC.
In den resultierenden Diagrammen werden einfach die bereits bekannten Grafiken erneut angezeigt, ergänzt um die Prüfung des Spektralmodells. Im Zusammenhang mit der Prüfung des Spektralmodells stellen die roten Kreise die Spektralschätzungen dar, und die schwarze durchgezogene Linie ist das „tatsächliche“ Spektrum auf der Grundlage der geschätzten ARIMA-Modellparameter. Die gepunkteten Linien stellen die Konfidenzgrenzen für das „tatsächliche“ Spektrum dar. Da fast alle der gleitenden Drei-Punkt-Durchschnitte (rote Kreise) innerhalb des Konfidenzintervalls für das tatsächliche Spektrum liegen, kann gefolgert werden, dass das Modell gültig ist. Abschließend sollte das Makro für die Residuen ausgeführt werden, um sicherzustellen, dass diese Residuen Zufallsrauschen darstellen. Das kumulative Periodogramm gibt auch tatsächlich an, dass die Residuen einem Zufallsrauschen entsprechen.
Literaturhinweise
Diggle, P. J. „Time Series, A Biostatistical Introduction“. Oxford: Clarendon Press, 1990.
