Herunterladen des Makros
Vergewissern Sie sich, dass Sie in Minitab den Speicherort des heruntergeladenen Makros angegeben haben. Wählen Sie aus. Navigieren Sie im Feld Speicherort für Makros zu dem Speicherort, an dem Sie Makrodateien ablegen.
Wichtig
Wenn Sie einen älteren Webbrowser verwenden und auf die Schaltfläche Herunterladen klicken, wird die Datei möglicherweise in Quicktime geöffnet; für dieses Programm wird dieselbe Dateinamenerweiterung „.mac“ wie für Minitab-Makros verwendet. Um das Makro zu speichern, klicken Sie mit der rechten Maustaste auf die Schaltfläche Herunterladen, und wählen Sie Ziel speichern unter aus.
Erforderliche Eingaben
Sie benötigen bis zu fünf Versuchsplanmatrizen.
Optionale Eingaben
- MODEL Modelltyp
- Gibt das Modell an, das bei Ausführung des Experiments getestet werden soll. Der Standardwert ist „interaction“ (Wechselwirkung). Sie können mehrere Modelle eingeben, z. B. „linear“, „quadratic“ (quadratisch), „interaction“ (Wechselwirkung) und „purequadratic“ (rein quadratisch). Die Modelle beinhalten die folgenden Terme:
- Linear: konstante und lineare Terme
- Wechselwirkung: konstante, lineare und Kreuzprodukt-Terme
- Quadratisch: Wechselwirkungen plus quadrierte Terme
- Rein quadratisch: konstante, lineare und quadratischen Terme
- RESOLUTION K
- Hiermit geben Sie die Anzahl der Versuchsplanpunkte aus der Stichprobe an, die zum Schätzen der minimalen, maximalen und der integrierten Prognosevarianz an jedem einzelnen Wert des Radius verwendet werden. Für drehbare Versuchspläne können Sie eine kleine Auflösung wählen. Für nicht drehbare Versuchspläne müssen Sie die Auflösung bei zunehmender Anzahl von Faktoren ggf. erhöhen. Der Standardwert ist 500 Versuchsplanpunkte.
- INCREMENT K
- Hiermit geben Sie das Radiusintervall an. Sie können diesen Wert ändern, um die Grafik mit einer größeren oder kleineren Auflösung anzuzeigen. Der Standardwert ist 0,1 kodierte Einheiten.
- MAXDIST K
- Gibt die maximale Radiusdistanz an. Diese ist standardmäßig als die größte Distanz zu dem Versuchsplanpunkt definiert, der am weitesten vom Mittelpunkt des Versuchsplans entfernt liegt. Für ein auf mehreren Versuchsplänen basierendes VDG ist MAXDIST als die größte Distanz aus allen Versuchsplänen festgelegt.
Ausführen des Makros
Angenommen, die Faktoren eines CCD wurden in die Matrix M1 kopiert, und die Faktoren eines Box-Behnken-Versuchsplans wurden in M2 gespeichert. Um das Makro auszuführen, wählen Sie aus, und geben Sie Folgendes ein:
%VDG M1 M2;
MODEL "quadratic";
RESOLUTION 150.Klicken Sie auf Durchlauf.
Weitere Informationen
Varianzen-Dispersionsdiagramme und Versuchsplanung
Varianzen-Dispersionsdiagramme sind grafische Werkzeuge, die bei der Auswahl eines Versuchsplans verwendet werden. Diese Grafiken zeigen die skalierte Prognosevarianz eines Versuchsplans im Raum des Versuchsplans und werden in der Regel zum Vergleichen von Wirkungsflächenversuchsplänen verwendet. Varianzen-Dispersionsdiagramme können jedoch auch zum Vergleichen der Leistung mehrerer Versuchspläne für ein bestimmtes Modell verwendet werden, z. B. eines linearen Modells, eines linearen Modells mit Wechselwirkungstermen, eines linearen Modells mit quadratischen Termen und eines vollständig quadratischen Modells.
Geschichte und Hintergrund von Varianzen-Dispersionsdiagrammen (VDG)
Das VDG wurde ursprünglich von Giovannitti-Jensen und Myers (1989) sowie Myers et al. (1992) entwickelt, um eine Momentaufnahme der Stabilität der skalierten Prognosevarianz im Raum des Versuchsplans anzuzeigen.
Mathematisch kann die skalierte Prognosevarianz mit folgender Gleichung geschätzt werden:
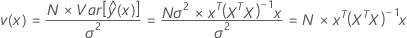
Hierbei ist v(x) die skalierte Prognosevarianz an Punkt x und, wie oben dargestellt, nicht von den Daten der Antwortvariablen, sondern nur von der Versuchsplanmatrix X abhängig. Mit anderen Worten, die skalierte Prognosevarianz ist eine Funktion der Anzahl der Durchläufe in Ihrem Experiment, der Kovarianzmatrix und des Punkts, an dem Sie die Prognosevarianz auswerten. Da die im VDG gezeigte skalierte Prognosevarianz unabhängig von den Daten der Antwortvariablen ist, ermöglicht Ihnen das VDG, die Güte eines Versuchsplans vorab auszuwerten.
Im allgemeinen besteht ein VDG aus vier grundlegenden Komponenten:
- Einem Diagramm der sphärischen Varianz im Vergleich zum Radius r. Die sphärische Varianz entspricht v(x) gemittelt (integriert) über die Oberfläche einer Kugel mit dem Radius r.
- · Einem Diagramm der maximalen Prognosevarianz auf einem Radius r für mehrere Werte von r, ausgehend vom Ursprung (r beginnt am Nullpunkt und nähert sich in kleinen Schritten dem am weitesten vom Ursprung entfernten Punkt im Versuchsplan an).
- · Einem Diagramm der minimalen Prognosevarianz auf einem Radius r für mehrere Werte von r, ausgehend vom Ursprung.
- · Einer horizontalen Linie bei v(x) = p, wobei p der Anzahl von Parametern im anzupassenden Modell entspricht. In einem „optimalen“ Design wäre die höchste Prognosevarianz für alle Punkte im Versuchsplanraum kleiner oder gleich p.
Das VDG zeigt die durchschnittlichen, maximalen und minimalen skalierten Prognosevarianzen an verschiedenen Werten von r, das den Abstand jedes gegebenen Punkts zum Ursprung bzw. zum Mittelpunkt des Versuchsplans darstellt.
Verwenden eines VDG zum Auswerten von anderen Aspekten eines Versuchsplans
Mit einem VDG können Sie die Leistung eines einzelnen Versuchsplans hinsichtlich dessen Prognosevarianz auswerten. Außerdem können Sie das VDG zum Vergleichen von zwei oder mehr Versuchsplänen nutzen. Eine weitere Anwendung eines VDG ist, die Auswirkungen auszuwerten, die auftreten, wenn einem Versuchsplan Zentralpunkte hinzugefügt werden.
Mit einem VDG können Sie außerdem auswerten, ob ein Versuchsplan drehbar ist. In einem drehbaren Versuchsplan überdecken sich alle drei Linien (Minimum, Durchschnitt und Maximum) in der Grafik. Wenn sich die Linien des Minimums, des Durchschnitts und des Maximums nicht überdecken, ist der flächenzentrierte Versuchsplan nicht drehbar.
Monte-Carlo-Simulation zur Schätzung der Prognosevarianz
In diesem fortgeschrittenen Abschnitt werden die mathematischen Methoden beschrieben, die zur Schätzung der in einem VDG gezeigten minimalen, maximalen und durchschnittlichen Prognosevarianzen angewendet werden. Wenn Sie lediglich daran interessiert sind, wie Sie ein Makro ausführen, um ein VDG zu erstellen und zu interpretieren, können Sie diesen Abschnitt überspringen.
Wie bereits erwähnt muss für einen festen Wert auf dem Radius eine Suche ausgeführt werden, um die minimale, die maximale und die integrierte skalierte Prognosevarianz zu bestimmen. Die für das Minitab-Makro ausgewählte Methode basiert auf der Monte-Carlo-Simulation und der Fähigkeit, einheitlich an gleich weit vom Mittelpunkt x = (0,0,…,0)T des Versuchsplans entfernten Punkten zu suchen.
Es müssen drei Größen für die verschiedenen Abstände vom Ursprung berechnet werden: 1) die minimale Prognosevarianz, 2) die maximale Prognosevarianz und 3) die integrierte Prognosevarianz. Es gibt mehrere Möglichkeiten, diese Größen zu ermitteln. Eine Methode besteht darin, die minimale und die maximale Prognosevarianz mit Hilfe eines nicht linearen Algorithmus zu ermitteln. Die von uns gewählte Methode zur Schätzung dieser Größen ist, einheitliche Punkte zu wählen und dabei eine große Gruppe eindeutiger Punkte zu finden, die für verschiedene Werte von r den gleichen Abstand vom Mittelpunkt des Versuchsplans haben. Aus dem Raum der äquidistanten Punkte kann die angemessene Schätzung der minimalen und maximalen Prognosevarianzen garantiert werden, indem zwei Bedingungen erfüllt werden: Erstens muss die Auswahl der äquidistanten Punkte einheitlich sein. Mit anderen Worten, es darf keine Bereiche geben, in denen äquidistante Punkte wahrscheinlicher ausgewählt werden als in anderen. Zweitens muss die Anzahl der Punkte groß genug sein, um den gesamten Raum der möglichen Punkte im Versuchsplan abzudecken.
Da alle Punkte, die möglicherweise ausgewählt werden, äquidistant sind, entspricht das Auswahlproblem einer guten Lösung für das Erfassen von Punkten von einer n-dimensionalen Kugel bzw. Hypersphäre mit einem angegebenen Radius.
Das Verfahren ist in Marsaglia (1972) beschrieben und nachfolgend zusammengefasst:
- Es wird ein n-dimensionaler Vektor aus normalverteilten Zufallsvariablen generiert (z. B. aus einer Standardnormalverteilung). Dieser Vektor sei x = (x1, x2, …, xn). Es werden mehrere Vektoren x erstellt.
- Der Radius ρ wird für alle generierten Punkte x berechnet.

- Die ursprünglichen Punkte im Versuchsplan aus Schritt 1 werden durch Multiplizieren der einzelnen Einträge von Vektor x mit r transformiert, wobei r für den Radius der Hypersphäre steht, aus der Sie die Punkte auswählen.
Wir haben gezeigt, wie Punkte von einer Hypersphäre mit dem konstanten Radius r ausgewählt werden. Mit diesem Auswahlverfahren kann die maximale bzw. die minimale Prognosevarianz geschätzt werden. Mit Hilfe dieser ausgewählten Punkte und auf der Grundlage des schwachen Gesetzes der großen Zahlen kann die durchschnittliche Prognosevarianz der ausgewählten Versuchsplanpunkte verwendet werden, um die wahre integrierte Prognosevarianz zu schätzen, sofern n groß ist.
Literaturhinweise
[1] Marsaglia, G. „Choosing a Point from the Surface of a Sphere“. The Annals of Mathematical Statistics, Vol. 43, No. 2 (1972), S. 645-646.
[2] Myers, R. und Montgomery, D. (2002). Response Surface Methodology – Process and Product Optimization Using Designed Experiments, Second Edition. John Wiley & Sons, Inc.
