Herunterladen des Makros
Vergewissern Sie sich, dass Sie in Minitab den Speicherort des heruntergeladenen Makros angegeben haben. Wählen Sie aus. Navigieren Sie im Feld Speicherort für Makros zu dem Speicherort, an dem Sie Makrodateien ablegen.
Wichtig
Wenn Sie einen älteren Webbrowser verwenden und auf die Schaltfläche Herunterladen klicken, wird die Datei möglicherweise in Quicktime geöffnet; für dieses Programm wird dieselbe Dateinamenerweiterung „.mac“ wie für Minitab-Makros verwendet. Um das Makro zu speichern, klicken Sie mit der rechten Maustaste auf die Schaltfläche Herunterladen, und wählen Sie Ziel speichern unter aus.
Erforderliche Eingaben
- Eine Spalte mit numerischen Daten der Antwortvariablen
- Eine entsprechende Spalte von Faktorstufen
Hinweis
Sie können ungestapelte Daten verwenden, indem Sie den Unterbefehl UNSTACKED angeben.
Optionale Eingaben
- UNSTACKED
- Geben Sie diesen Unterbefehl an, wenn die Daten ungestapelt sind.
- FALPHA
- Hiermit geben Sie das gewünschte simultane Alpha-Niveau an (das Standardniveau ist 0,20).
- CONTROL C
- Hiermit geben Sie eine Spalte (C) als Kontrollspalte an.
Hinweis
Wenn die Daten gestapelt sind, darf sich die Antwortvariable für die Kontrollgruppe nicht in derselben Spalte wie die Antwortvariable für die übrigen Faktorstufen befinden. Die Antwortvariable für die Kontrollgruppe muss sich in einer separaten Spalte befinden.
Ausführen des Makros
Angenommen, die Daten der Antwortvariablen befinden sich in C1, und die Faktorstufen sind in C2 enthalten. Um das Makro auszuführen, wählen Sie aus, und geben Sie Folgendes ein:
%KRUSMC C1 C2Klicken Sie auf Durchlauf.
Ausgabe
Der erste Teil der Ausgabe zeigt die Anzahl der durchgeführten Vergleiche (k),
 , das simultane Alpha (α), das individuelle Alpha nach Bonferroni (β),
, das simultane Alpha (α), das individuelle Alpha nach Bonferroni (β),  , und den zweiseitigen kritischen z-Wert.
, und den zweiseitigen kritischen z-Wert.
Im nächsten Abschnitt werden die Rangfolgendifferenzen in den standardisierten Gruppenmittelwerten (θ) und die p-Werte für diese Differenzen angezeigt. Beachten Sie, dass diese Tabellen symmetrisch sind, so dass im oberen dreieckigen Teil der Tabelle Sternchen enthalten sind. Entlang der Tabellendiagonalen nach unten sind Nullen aufgeführt, da die Diagonale einen Vergleich einer Gruppe mit sich selbst darstellt (derartige Vergleiche sind bedeutungslos und werden daher in der Analyse nicht berücksichtigt). Ein Beispiel zur Auswertung dieser Tabelle: Welche Differenz besteht zwischen den Gruppen 2 und 4? Im dritten Abschnitt werden Konfidenzintervalle mit Vorzeichen für die Mediane angezeigt. Die Konfidenzniveaus für diese Intervalle basieren auf dem angegebenen simultanen Alpha. Da diese Intervalle anhand des simultanen Alpha-Gesamtniveaus gehalten werden, können diese Intervalle paarweise verglichen werden (Anhang 2). Es ist unbedingt zu beachten, dass die gewünschte Konfidenz möglicherweise bei allen oder bestimmten Intervallen nicht erzielt werden kann. Diese „Gesamtabdeckung“ durch das simultane Alpha ist zudem nicht genau, wenn sich die Stichprobenumfänge unterscheiden; häufig stellt sie jedoch eine akzeptable Annäherung dar.
Im letzten Abschnitt werden die „signifikanten“ Differenzen angezeigt (sofern vorhanden). In diesem Abschnitt werden der z-Wert, der kritische z-Wert und der p-Wert für den z-Wert angegeben.
In der Grafik werden die nicht absoluten Rangfolgendifferenzen in den standardisierten Gruppenmittelwerten veranschaulicht. Diese Grafik ist äußerst nützlich, da nicht nur die Größe der Differenzen zwischen Gruppen, sondern auch die Richtung betrachtet werden kann. Zudem werden der positive und der negative kritische z-Wert angezeigt, so dass Sie feststellen können, ob eine Differenz „signifikant“ ist.
Bindungen in den Daten
Wenn Bindungen in den Daten vorliegen, wird eine erwartungstreue Konstante bzw. ein Korrekturfaktor (2) berechnet. Die H-Statistik wird dann korrigiert (3). Die Standardabweichung (ξ) wird ebenfalls anhand dieses Korrekturfaktors korrigiert (4). Die Ausgabe enthält sowohl die korrigierten als auch die nicht korrigierten Tabellen. Es werden jedoch lediglich p-Werte für die korrigierten Tabellen aufgeführt, da diese Tabellen verwendet werden sollten. Die nicht korrigierten Tabellen werden hauptsächlich gezeigt, um die Effekte der Bindungen auf die z-Werte darzustellen. Bei sehr vielen Bindungen sollte die Gültigkeit der Daten in Frage gestellt werden, da für diese Tests angenommen wird, dass die Verteilungen stetig sind. Häufig haben Bindungen jedoch nur eine geringfügige oder überhaupt keine Auswirkung auf Ihre Schlussfolgerungen.
Danksagung
Vielen Dank an Dr. Tom Hettmansperger (The Pennsylvania State University) für seine kritische Auswertung dieses Makros, unsere vielen Diskussionen über diese Arbeit sowie generell für seine Hilfe und seine Geduld. Mein Dank geht auch an Nicholas Bolgiano und Mike Delozier (Minitab, Inc.) für ihre Vorschläge und kritischen Anmerkungen zum Makro.
Weitere Informationen
Dunn-Test
Eine effektive Möglichkeit, paarweise simultane Rückschlüsse zu ziehen, wurde von Dunn (1964) vorgestellt. Zunächst werden die Daten kombiniert und in eine Rangfolge gebracht, die Ränge der Gruppenmittelwerte werden gebildet, und anschließend werden die standardisierten absoluten Differenzen dieser Mittelwert-Ränge bestimmt.
Sei k = Anzahl der Behandlungen, 
Sei 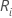 = Summe der Ränge für die i-te Behandlung, i = 1, …, k
= Summe der Ränge für die i-te Behandlung, i = 1, …, k
Sei 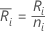
Hierbei ist 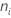 = Anzahl der Beobachtungen für die i-te Behandlung
= Anzahl der Beobachtungen für die i-te Behandlung
Sei 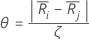
Hierbei ist j=l, ..., k und j  i
i
Hierbei ist 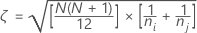
H-Statistik
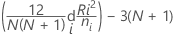
Hierbei ist 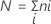
Dann wird Signifikanz festgestellt, wenn:

Hierbei ist 
Hierbei ist α ein angegebener simultaner Alpha-Wert, 
