Ein Qualitätsingenieur in einer Motorenfabrik möchte einen Test auf Bimodalität an Kolben von zwei Lieferanten durchführen. Der Ingenieur misst die Längen einer Stichprobe von je 100 Kolben von jedem der Lieferanten.
Das Skript verwendet das Paket diptest für R, um zu testen, ob die Daten unimodal sind. Wenn der Test die Nullhypothese für unimodale Daten ablehnt, geht das Skript davon aus, dass es sich bei den Daten um eine Mischung aus zwei Normalverteilungen handelt. Das Skript verwendet das Paket mixtools für R, um deskriptive Statistiken und Dichtekurven für zwei Normalverteilungen anzuzeigen.
- Übergeben Sie eine einzelne Spalte aus einem Minitab-Arbeitsblatt als Eingabe.
- Fügen Sie einen Tabellentitel hinzu.
- Fügen Sie Spaltenbeschriftungen für eine Tabelle hinzu.
- Senden Sie eine Tabelle an den Minitab-Ausgabebereich.
- Erstellen Sie ein Diagramm, und senden Sie das Diagramm an den Minitab-Ausgabebereich.
| Datei | Beschreibung |
|---|---|
| bimodal.R | Ein R Skript, das eine Spalte aus einem Minitab-Arbeitsblatt verwendet, auf Unimodalität testet und Ergebnisse für eine Mischung aus zwei Normalverteilungen erzeugt, wenn die Daten nicht unimodal sind. |
Alle Dateien, auf die in diesem Handbuch verwiesen wird, sind in dieser .ZIP-Datei verfügbar: r_guide_files.zip.
Voraussetzungen
-
Das R-Skript im folgenden Beispiel erfordert die folgenden R-Pakete:
- mtbr
- Das R-Paket, das Minitab und R integriert. Im Beispiel übertragen Funktionen aus diesem Modul R-Ergebnisse an Minitab. Informationen zum Installieren des Minitab-Pakets R finden Sie in Schritt 2: Installieren Sie mtbr.
- mixtools
- Das R Paket, das das Skript verwendet, um eine Ausgabe für eine Mischung von Normalverteilungen zu erstellen.
- diptest
- Das R Paket, das das Skript verwendet, um zu testen, ob die Daten unimodal sind.
install.packages("mixtools")Wenn Sie Hilfe bei der Installation von Paketen R benötigen, wenden Sie sich bitte an den technischen Support Ihres Unternehmens. Der technische Support von Minitab kann Sie nicht bei der Installation von R Paketen unterstützen.
Schritte zum Ausführen des Beispiels
- Stellen Sie sicher, dass Sie die erforderlichen Module installiert haben: mtbr.
- Speichern Sie die R-Skriptdatei, bimodal.R in Ihrem Minitab-Standardspeicherort für Dateien. Weitere Informationen dazu, wo Minitab nach R-Skriptdateien sucht, finden Sie unter Standardordner für R-Dateien für Minitab.
- Öffnen Sie den Beispieldatensatz Prozessenergiekosten.MWX.
-
Geben Sie im Minitab-Fenster Befehlszeile
RSCR "bimodal.R" "Process 1"ein. - Wählen Sie Durchlauf aus.
bimodal. R
# Load the necessary libraries
#Original code by Valentina Tillman
library(mixtools)
library(mtbr)
library(diptest)
# Retrieve sample data
input_column <- commandArgs(trailingOnly = TRUE)
data <- mtb_get_column(input_column)
dip_test_result <- dip.test(data)
if (dip_test_result$p.value < 0.05) {
# Fit a bimodal mixture model
bimodal_fit <- normalmixEM(data, k = 2)
# Manually extract parameter estimates and format them as a data frame
bimodal_table <- data.frame(
Mean = bimodal_fit$mu,
Standard_Deviation = bimodal_fit$sigma,
Proportion = bimodal_fit$lambda #tells you what % of the data is clustered around which mean. Also called lambda
)
# Define title and headers
mytitle <- "Modeling a Bimodal Distribution"
myheaders <- names(bimodal_table)
# Add the table to the mtbr output
mtb_add_table(columns = bimodal_table, headers = myheaders, title = mytitle)
png("r_bimodal_image.png")
plot(bimodal_fit, density = TRUE, which = 2)
graphics.off()
mtb_add_image("r_bimodal_image.png")
# Now generate tolerance intervals using the parameters found using mixtools
# Set the desired coverage level (e.g., 95%)
coverage_level <- 0.95
alpha <- 1 - coverage_level
# Calculate the tolerance intervals for each component
tolerance_intervals <- lapply(1:2, function(i) {
mu <- bimodal_fit$mu[i]
sigma <- bimodal_fit$sigma[i]
n <- bimodal_fit$lambda[i] # proportion of the component
# Calculate the critical value for the normal distribution
z <- qnorm(1 - alpha / (2 * n))
# Calculate lower and upper bounds of the tolerance interval
lower_bound <- mu - z * sigma
upper_bound <- mu + z * sigma
c(lower_bound, upper_bound)
})
# Show the tolerance intervals
tolerance_intervals_df <- data.frame(
Component = c("First Mode", "Second Mode"),
Lower_Bound = sapply(tolerance_intervals, "[", 1),
Upper_Bound = sapply(tolerance_intervals, "[", 2)
)
myheaders <- c("Component", "Lower Bound", "Upper Bound")
mytitle <- "Tolerance Intervals for Bimodal Distribution"
mtb_add_table(columns = tolerance_intervals_df, headers = myheaders, title = mytitle)
} else {
mtb_add_message("This data is unimodal.")
}
Ergebnisse
Modeling a Bimodal Distribution
| Mean | Standard_Deviation | Proportion |
|---|---|---|
| 34.1875 | 1.50909 | 0.516129 |
| 48.3333 | 1.84992 | 0.483871 |
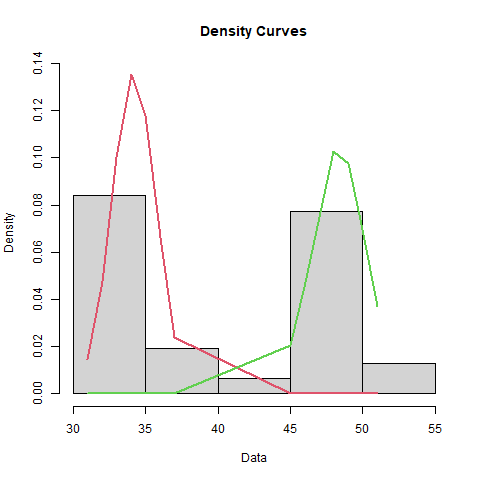
Tolerance Intervals for Bimodal Distribution
| Component | Lower Bound | Upper Bound |
|---|---|---|
| First Mode | 31.6821 | 36.6929 |
| Second Mode | 45.3200 | 51.3467 |
