Methoden und Formeln für den Test für 2x2-Tabellen für Kreuztabelle und Chi-Quadrat-Test

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Fishers exakter Test
McNemars exakter Test
Cochran-Mantel-Haenszel-Test

Fishers exakter Test

Fishers exakter Test ist ein Test auf Unabhängigkeit. Der Test beruht auf einer exakten Verteilung und nicht auf der näherungsweisen Chi-Quadrat-Verteilung, die für die Pearson- und Likelihood-Quotienten-Tests verwendet wird. Fishers exakter Test ist hilfreich, wenn die erwarteten Zellenanzahlen gering sind und die Chi-Quadrat-Approximation nicht sehr gut geeignet ist.

Formel

Der p-Wert beruht auf einer hypergeometrischen Verteilung mit den folgenden Parametern:

Größe der Grundgesamtheit: Gesamtzahl der Beobachtungen
Anzahl der Erfolge in der Grundgesamtheit: Anzahl der Beobachtungen in der ersten Zeile
Stichprobenumfang: Anzahl der Beobachtungen in der ersten Spalte

Der p-Wert gilt für eine beidseitige Alternative. Die Berechnung ist die Summe der hypergeometrischen Wahrscheinlichkeiten für die Werte von 0 bis zur Größe der Grundgesamtheit, die kleiner oder gleich der Wahrscheinlichkeit des beobachteten Werts sind.

Beispiel

Angenommen, Sie möchten den p-Wert für Fishers exakten Test für die Keksvorlieben von Erwachsenen und Kindern berechnen.

	Kind	Erwachsener	Zeilengesamtwert
Zucker	9	1	10
Schokoladenstückchen	2	8	10
Spaltengesamtwert	11	9	20

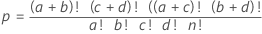
Der Fisher-Test hat gezeigt, dass die Wahrscheinlichkeit, diese Gruppe von Werten zu erhalten, der hypergeometrischen Verteilung folgt:

Dies sieht im Beispiel wie folgt aus:

	Kind	Erwachsener	Zeilengesamtwert
Zucker	a	b	a+b
Schokoladenstückchen	c	d	c+d
Spaltengesamtwert	a+c	b+d	a+b+c+d

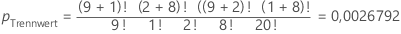
Im Fall einer 2x2-Matrix können Sie den p-Wert des Tests berechnen, indem Sie alle p-Werte summieren, die kleiner als die bedingte Wahrscheinlichkeit der tatsächlichen Matrix sind. Somit ist p_Trennwert:

In diesem Beispiel ist die Summe der p-Werte, die kleiner als oder gleich p_Trennwert für die anderen möglichen Matrizen sind, gleich 0,0054775.

McNemars exakter Test

Mit dem McNemar-Test werden Anteile verglichen, die vor und nach einer Behandlung beobachtet werden. Sie können mit dem McNemar-Test beispielsweise feststellen, ob sich durch ein Schulungsprogramm der Anteil der Teilnehmer ändert, die eine Frage richtig beantworten.

Beobachtungen für einen McNemar-Test können in einer 2x2-Tabelle wie nachfolgend gezeigt zusammengefasst werden.

	Nach der Behandlung
Vor der Behandlung	Bedingung wahr	Bedingung nicht wahr	Gesamt
Bedingung wahr	n₁₁	n₁₂	n_{1_.}
Bedingung nicht wahr	n₂₁	n₂₂	n_{2_.}
Gesamt	n_·1	n_·2	n_··

Die Bedingung für das Schulungsbeispiel ist eine korrekte Antwort. Daher steht n₂₁ für die Anzahl der Teilnehmer, die die Frage nach der Schulung korrekt beantworten, jedoch nicht vor der Schulung. Und n₁₂ steht für die Anzahl der Teilnehmer, die die Frage vor der Schulung korrekt beantworten, jedoch nicht nach der Schulung. n_.. steht für die Gesamtzahl der Teilnehmer.

Geschätzte Differenz

Sei δ die Differenz zwischen den Randwahrscheinlichkeiten p_1.– p_.1 in der Grundgesamtheit. Die geschätzte Differenz wird mit der folgenden Formel angegeben:

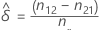
Konfidenzintervall

Ein ungefähres 100(1 – α)%-Konfidenzintervall wird durch die folgende Formel angegeben:

Hierbei ist α das Signifikanzniveau für den Test, z _α/2 der z-Wert, der einer Wahrscheinlichkeit α/2 im Randbereich zugeordnet ist, und SE wird durch die folgende Formel angegeben:

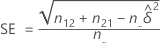
p-Wert

Die Nullhypothese ist δ = 0. Der exakte p-Wert für den Test der Nullhypothese wird wie folgt berechnet:

Dabei ist X eine Zufallsvariable, die einer Binominalverteilung entnommen wird, mit der Ereigniswahrscheinlichkeit 0,5 und der Anzahl von Versuchen = n₂₁ + n₁₂.

Cochran-Mantel-Haenszel-Test

Für den Test wird die Annahme getroffen, dass keine Drei-Faktor-Wechselwirkung vorhanden ist. Zweck des Tests ist es, den Grad der Beziehung zwischen zwei dichotomen Variablen bei gleichzeitiger Berücksichtigung einer Störvariable auszuwerten. Die CMH-Statistik wird mit einem Chi-Quadrat-Perzentil mit einem Freiheitsgrad verglichen.

Der Cochran-Mantel-Haenszel-Test (CMH) kann nur verwendet werden, wenn drei oder mehr Klassifikationsvariablen vorhanden sind und die ersten zwei Variablen jeweils über zwei Stufen verfügen. Alle Variablen, die über die ersten beiden hinausgehen, werden hinsichtlich des CMH-Tests als eine einzelne Variable Z behandelt, wobei jede Kombination aus Stufen als eine Stufe von Z behandelt wird.

Formel

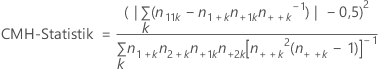
Notation

Begriff	Beschreibung
k	Stufe von Z
n_11k	Anzahl der Beobachtungen in der ersten Zeile, erste Spalte
n_1+k	Anzahl der Beobachtungen in der ersten Zeile
n_+1k	Anzahl der Beobachtungen in der ersten Spalte
n_++k	Gesamtzahl der Beobachtungen
n_2+k	Anzahl der Beobachtungen in der zweiten Zeile
n_+2k	Anzahl der Beobachtungen in der zweiten Spalte