Methoden und Formeln für die Konkordanzmaße für Kreuztabelle und Chi-Quadrat-Test

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Anzahl konkordanter und diskordanter Paare
Gamma
Somers-D
Kendall-Tau-b
Prüfung der Konkordanz

Anzahl konkordanter und diskordanter Paare

Ein Paar ist konkordant, wenn die Beobachtung, die bezüglich Variable x höher eingestuft wird, auch bezüglich Variable y höher eingestuft wird. Das Paar ist diskordant, wenn die Beobachtung, die bezüglich Variable x höher eingestuft wird, bezüglich Variable y niedriger eingestuft wird. Das Paar ist gebunden, wenn die Versuchspersonen dieselbe Klassifizierung bezüglich x und/oder y aufweisen.

Formel

Notation

Begriff	Beschreibung
n_ij	Beobachtungen in der Zelle, die der i-ten Zeile und der j-Spalte entspricht

Gamma

Das Goodman-Kruskal-Gamma ist ein Maß der Assoziation zwischen den ordinalen Variablen. Eine perfekte Assoziation besteht, wenn |γ| = 1. Wenn x und y unabhängig sind, ist γ = 0.

Formel

Notation

Begriff	Beschreibung
C	Anzahl der konkordanten Paare = Σ_i<kΣ_j<l n_ij n_kl
D	Anzahl der diskordanten Paare = Σ_i<kΣ_j>l n_ij n_kl
n_ij	Beobachtungen in der Zelle, die der i-ten Zeile und der j-Spalte entspricht

Somers-D

Mit dem Somers-D wird die Stärke und Richtung der Beziehung zwischen zwei ordinalen Variablen gemessen.

Formel

Mit y als Antwortvariable:

Mit x als Antwortvariable:

Notation

Begriff	Beschreibung
T_X	Anzahl der gebundenen Paare bei x =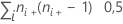
T_Y	Anzahl der gebundenen Paare bei y =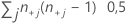
C	Anzahl der konkordanten Paare
D	Anzahl der diskordanten Paare
n_i+	Anzahl der Beobachtungen in der i-ten Zeile
n_+j	Anzahl der Beobachtungen in der j-ten Spalte
n_ij	Beobachtungen in der Zelle, die der i-ten Zeile und der j-Spalte entspricht
n₊₊	Gesamtzahl der Beobachtungen

Kendall-Tau-b

Mit dem Kendall-Tau-b wird wie mit dem Gamma die Assoziation zwischen ordinalen Variablen gemessen. Eine Stärke von Kendall-Tau-b als Assoziationsmaß ist, dass gebundene Paare bei der Berechnung berücksichtigt werden. Bei dem Gamma sind gebundene Paaren problematisch, weshalb das Gamma fast immer eine höhere Assoziation als das Tau-b ausweist. Das Tau-b kann Werte von -1,0 bis 1,0 annehmen.

Formel

Notation

Begriff	Beschreibung
T_X	Anzahl der gebundenen Paare bei x = Σ_i n_i+ (n_i+– 1) 0,5
T_Y	Anzahl der gebundenen Paare bei y = Σ_j n_+j (n_+j– 1) 0,5
C	Anzahl der konkordanten Paare = Σ_i<kΣ_j<l n_ij n_kl
D	Anzahl der diskordanten Paare = Σ_i<kΣ_j>l n_ij n_kl
n_i+	Anzahl der Beobachtungen in der i-ten Zeile
n_+j	Anzahl der Beobachtungen in der j-ten Spalte
n_ij	Beobachtungen in der Zelle, die der i-ten Zeile und der j-Spalte entspricht
n₊₊	Gesamtzahl der Beobachtungen

Prüfung der Konkordanz

Der Konkordanztest ist ein Test der Unabhängigkeit. Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.

Formel

Für den Konkordanztest wird eine Standard-Normalteststatistik verwendet:

Der p-Wert entspricht der Wahrscheinlichkeit, dass Z größer als Z* ist.

Notation

Begriff	Beschreibung
C	Anzahl der konkordanten Paare = Σ_i<kΣ_j<l n_ij _{n kl}
D	Anzahl der diskordanten Paare = Σ_i<kΣ_j>l n_ij _{n kl}
SE(C-D)	Standardfehler oder C-D, der ungefähr gleich ist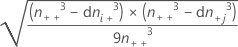
n₊₊	Gesamtzahl der Beobachtungen
n_i+	Die Anzahl der Beobachtungen in der i^-ten Zeile.
n_+j	Die Anzahl der Beobachtungen in der Spalte J-T .