Methoden und Formeln für Chi-Quadrat-Test auf Assoziation

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Chi-Quadrat-Teststatistik
Erwartete Zellenanzahl
Berechnung des Rohresiduums
Berechnung des standardisierten Residuums
Berechnung des korrigierten Residuums
Beitrag jeder Zelle zur Chi-Quadrat-Statistik

Chi-Quadrat-Teststatistik

Minitab zeigt zwei Chi-Quadrat-Statistiken an.

Chi-Quadrat-Statistik nach Pearson:

Likelihood-Quotienten-Chi-Quadrat-Statistik:

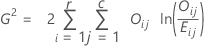
Hinweis

Wenn eine Zelle eine erwartete Häufigkeit von kleiner als 1 aufweist, wird der p-Wert für den Test nicht angezeigt, da die Ergebnisse möglicherweise nicht gültig sind. Wenn einige Zellen geringe erwartete Häufigkeiten aufweisen, können Sie Zeilen- und/oder Spaltenkategorien kombinieren oder auslassen.

Die Yates-Korrektur für 2x2-Tabellen wird nicht verwendet.

Notation

Begriff	Beschreibung
O_ij	beobachtete Häufigkeit in Zelle (i, j)
E_ij	erwartete Häufigkeit für Zelle (i, j)
r	Anzahl der Zeilen
c	Anzahl der Spalten

Eine Kontingenztafel mit r Zeilen und c Spalten weist (r – 1)(c – 1) Freiheitsgrade auf.

Erwartete Zellenanzahl

Die erwartete Anzahl ist die in einer Zelle durchschnittlich zu erwartende Häufigkeit, wenn die Variablen unabhängig wären. Minitab berechnet die erwarteten Anzahlen als das Produkt aus den Zeilen- und Spaltensummen geteilt durch die Gesamtzahl der Beobachtungen.

Formel

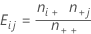
Notation

Begriff	Beschreibung
n_i+	Anzahl der Beobachtungen in der i-ten Zeile
n_+j	Anzahl der Beobachtungen in der j-ten Spalte
n₊₊	Gesamtzahl der Beobachtungen

Berechnung des Rohresiduums

Formel

Rohresiduum = O_ij – E_ij

Notation

Begriff	Beschreibung
O_ij	beobachtete Häufigkeit in Zelle (i, j)
E_ij	erwartete Häufigkeit für Zelle (i, j)

Berechnung des standardisierten Residuums

Formel

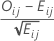
Notation

Begriff	Beschreibung
O_ij	beobachtete Häufigkeit in Zelle (i, j)
E_ij	erwartete Häufigkeit für Zelle (i, j)

Berechnung des korrigierten Residuums

Formel

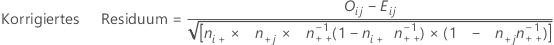
Notation

Begriff	Beschreibung
O_ij	beobachtete Häufigkeit in Zelle (i, j)
E_ij	erwartete Häufigkeit für Zelle (i, j)
n_i+	Anzahl der Beobachtungen in der i-ten Zeile
n_+j	Anzahl der Beobachtungen in der j-ten Spalte
n₊₊	Gesamtzahl der Beobachtungen

Beitrag jeder Zelle zur Chi-Quadrat-Statistik

Formel

Der Beitrag jeder Zelle zur χ²-Statistik ist:

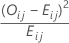
Notation

Begriff	Beschreibung
O_ij	beobachtete Häufigkeit in Zelle (i, j)
E_ij	erwartete Häufigkeit für Zelle (i, j)