Wählen Sie die gewünschte Methode oder Formel aus.
In diesem Thema
Erwarteter Wert für jede Kategorie
Formel
Der erwartete Wert E für jede Kategorie i wird wie folgt berechnet:
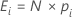
Notation
| Begriff | Beschreibung |
|---|---|
| pi | Testanteil für die i-te Kategorie, was 1/k oder dem von Ihnen angegebenen Wert entspricht |
| k | Anzahl der eindeutigen Kategorien |
| N | beobachtete Werte gesamt (O1 + ... + Ok) |
| Oi | beobachteter Wert für die i-te Kategorie |
Chi-Quadrat-Teststatistik
Formel
Die Chi-Quadrat-Teststatistik wird wie folgt berechnet:
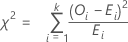
Notation
| Begriff | Beschreibung |
|---|---|
| k | Anzahl der eindeutigen Kategorien |
| Oi | beobachteter Wert für die i-te Kategorie |
| Ei | erwarteter Wert für die i-te Kategorie |
Beitrag zur Chi-Quadrat-Statistik
Formel
Der Beitrag der i-ten Kategorie zum Chi-Quadrat-Wert ist:

Notation
| Begriff | Beschreibung |
|---|---|
| Oi | beobachteter Wert für die i-te Kategorie |
| Ei | erwarteter Wert für die i-te Kategorie |
Freiheitsgrade (DF)
Formel
Die Freiheitsgrade (DF) werden wie folgt berechnet:

Notation
| Begriff | Beschreibung |
|---|---|
| DF | Freiheitsgrade |
| k | Anzahl der Kategorien |
p-Wert
Formel
Der p-Wert wird wie folgt berechnet: Wahrsch (X > Teststatistik)
Notation
| Begriff | Beschreibung |
|---|---|
| X | folgt einer Chi-Quadrat-Verteilung mit k – 1 Freiheitsgraden |
Beispielberechnung
Gegeben:
| Kategorie i | Beobachtet Oi | Testanteile pi |
|---|---|---|
| A | 5 | 0,1 |
| B | 15 | 0,2 |
| C | 10 | 0,3 |
| D | 10 | 0,4 |
| N=40 |
Berechnet:
| Kategorie i | Erwarteter Wert
Ei = (pi * N) |
Beitrag zu Chi-Quadrat
(Oi – Ei)2 / Ei |
|---|---|---|
| A | 0,1 * 40 = 4 | (5 – 4)2 / 4 = 0,2500 |
| B | 0,2 * 40 = 8 | (15 – 8)2 / 8 = 6,1250 |
| C | 0,3 * 40 = 12 | (10 – 12)2 / 12 = 0,3333 |
| D | 0,4 * 40 = 16 | (10 – 16)2 / 16 = 2,25 |
χ2 = 0,2500 + 6,1250 + 2,2500 + 0,3333 = 8,9583
DF = k – 1 = 3
p-Wert = Wahrsch(Χ > 8,9583) = 0,0299
Notation
| Begriff | Beschreibung |
|---|---|
| DF | Freiheitsgrade |
| k | Anzahl der Kategorien |
