In diesem Thema
Mittelwert (normal)
Standardabweichung ist bekannt
Das Konfidenzintervall für einen Mittelwert aus einer Normalverteilung entspricht bei bekannter Standardabweichung der Grundgesamtheit:

Die Fehlerspanne ist gleich 
Auflösen für n:

Standardabweichung ist nicht bekannt
Das Konfidenzintervall für einen Mittelwert aus einer Normalverteilung entspricht bei unbekannter Standardabweichung der Grundgesamtheit:
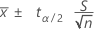
Die Fehlerspanne ist gleich 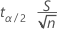
Berechnen Sie zum Auflösen für n den minimalen Wert für n, so dass Folgendes gilt:
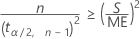
Notation
| Begriff | Beschreibung |
|---|---|
 | Mittelwert der Stichprobe |
| zα/2 | inverse kumulative Wahrscheinlichkeit der Standardnormalverteilung bei 1- α /2; α = 1 - Konfidenzniveau/100 |
| σ | Standardabweichung der Grundgesamtheit (als bekannt angenommen) |
| n | Stichprobenumfang |
| ME | Fehlerspanne |
| t α/2 | inverse kumulative Wahrscheinlichkeit einer t-Verteilung mit n-1 Freiheitsgraden bei 1-α/2 |
| S | Planwert |
Anteil (Binomial)
Untergrenze
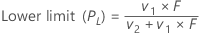
Obergrenze
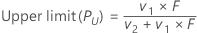
Das Intervall (PU, PO) ist ein ungefähres 100(1 – α)%-Konfidenzintervall von p.
Hinweis
Berechnen Sie zum Auflösen für n den minimalen Wert für n, so dass Folgendes gilt:
Notation
| Begriff | Beschreibung |
|---|---|
| v1 (Untergrenze) | 2x |
| v2 (Untergrenze) | 2(n – x + 1) |
| v1 (Obergrenze) | 2(x + 1) |
| v2 (Obergrenze) | 2(n – x) |
| x | Anzahl der Ereignisse |
| n | Anzahl der Versuche |
| F (Untergrenze) | unterer α/2-Punkt der F-Verteilung mit v1 und v2 Freiheitsgraden |
| F (Obergrenze) | oberer α/2-Punkt der F-Verteilung mit v1 und v2 Freiheitsgraden |
Rate und Mittelwert (Poisson)
Formel
Das Konfidenzniveau der Untergrenze für eine Rate oder einen Mittelwert aus einer Poisson-Verteilung wird wie folgt ausgedrückt:
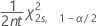
Das Konfidenzniveau der Obergrenze für eine Rate oder einen Mittelwert aus einer Poisson-Verteilung wird wie folgt ausgedrückt:
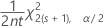
Die untere Fehlerspanne ist gleich −1 × (Konfidenzniveau der Untergrenze). Die obere Fehlerspanne ist gleich dem Konfidenzniveau der Obergrenze.
Berechnen Sie zum Auflösen für n den minimalen Wert für n, so dass Folgendes gilt:
(S – SU) ≤ ME und (SO – S) ≤ ME
Notation
| Begriff | Beschreibung |
|---|---|
| n | Stichprobenumfang |
| t | Beobachtungsumfang; für den Poisson-Mittelwert gilt, dass der Umfang = 1 |
| s | Gesamt-Ereignishäufigkeit in einem Poisson-Prozess |
| χ2p, x | oberer x-ter Perzentilpunkt einer Chi-Quadrat-Verteilung mit p Freiheitsgraden, wobei 0 < x < 1 |
| S | Planwert |
| ME | Fehlerspanne |
Varianz und Standardabweichung (normal)
Formel
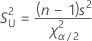
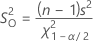
Um das Konfidenzintervall für die Standardabweichung zu erhalten, ziehen Sie die Quadratwurzel der obigen Gleichungen.
Die untere Fehlerspanne ist gleich −1 × (Konfidenzniveau der Untergrenze). Die obere Fehlerspanne ist gleich dem Konfidenzniveau der Obergrenze.
Berechnen Sie zum Auflösen von n für die Varianz den minimalen Wert für n, so dass Folgendes gilt:
(S2 – S2U) ≤ ME und (S2O – S2) ≤ ME
Berechnen Sie zum Auflösen für n für die Standardabweichung den minimalen Wert für n, so dass Folgendes gilt:
(S – SU) ≤ ME und (SO – S) ≤ ME
Notation
| Begriff | Beschreibung |
|---|---|
| n | Stichprobenumfang |
| s2 | Stichprobenvarianz |
| Χ2 p | oberer 100p-ter Perzentilpunkt in einer Chi-Quadrat-Verteilung mit (n – 1) Freiheitsgraden |
| S | Planwert |
| ME | Fehlerspanne |
