Methoden und Formeln für Trennschärfe und Stichprobenumfang für Plackett-Burman-Versuchsplan

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Berechnen der Trennschärfe
Berechnen der Replikationen, Effekte und Zentralpunkte
Nichtzentralitätsparameter

Berechnen der Trennschärfe

In Minitab wird angenommen, dass keine Textfaktoren und damit keine Pseudozentralpunkte vorhanden sind.

Minitab berechnet zuerst die Freiheitsgrade für den Fehler (v).

Freiheitsgrade für Fehler: ν = (Gesamtzahl der Beobachtungen – Anzahl der geschätzten Parameter); Gesamtzahl der Beobachtungen = n * r + c; Anzahl der geschätzten Parameter = (Anzahl der Faktoren + 1) + 1 (wenn der Term für Zentralpunkte eingeschlossen ist) – (Anzahl der Terme für Haupteffekte, die aus dem Modell entfernt wurden)
Trennschärfe

Notation

Begriff	Beschreibung
n	Anzahl der Replikationen
r	Anzahl der Durchläufe an den Eckpunkten pro Replikation
c	Anzahl der Zentralpunkte
α	Signifikanzniveau
v	Freiheitsgrade für Fehler
λ	Nichtzentralitätsparameter
f_α	kritischer Wert (oberer α-Punkt der F-Verteilung mit 1 und ν Freiheitsgraden)
F(f_α ; 1, v, λ)	CDF der F-Verteilung mit 1 Freiheitsgrad des Zählers, v Freiheitsgraden des Nenners und Nichtzentralitätsparameter λ, ausgewertet bei f_α

Berechnen der Replikationen, Effekte und Zentralpunkte

Wenn Sie Werte für die Trennschärfe und zwei andere Eigenschaften angeben, berechnet Minitab die unbekannte vierte Eigenschaft, indem die Trennschärfegleichung iterativ angewendet wird. Bei jeder Iteration wertet Minitab die Trennschärfe für die Werte der angegebenen Eigenschaften und einen Versuchswert der nicht angegebenen Maßzahl aus. Minitab beendet die Berechnungsprozedur, wenn der Algorithmus den angegebenen Trennschärfewert erreicht.

Wenn Sie einen Trennschärfewert angeben, ermittelt Minitab möglicherweise, dass die Soll-Trennschärfe nicht mit einem ganzzahligen Wert für die Anzahl der Replikationen erreicht wird. In diesem Fall zeigt Minitab den Sollwert für die Trennschärfe neben der tatsächlichen Trennschärfe an, die anhand Ihrer Angaben erreicht wird. Die Ist-Trennschärfe ist ein Wert, der der Soll-Trennschärfe am nächsten kommt, jedoch größer als diese ist.

Nichtzentralitätsparameter

Formel

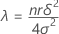
Notation

Begriff	Beschreibung
r	Anzahl der Durchläufe an den Eckpunkten pro Replikation
n	Anzahl der Replikationen
σ	geschätzte Standardabweichung
δ	Effekt
λ	Nichtzentralitätsparameter