Ein Qualitätstechniker plant einen Versuchsplan zum Untersuchen der Transparenz eines Kunststoffteils. Vor dem Experiment möchte er sicherstellen, dass das Experiment eine ausreichende Trennschärfe aufweist. Der Techniker beabsichtigt, zehn numerische Faktoren zu untersuchen. Als Basisversuchsplan wählt er einen Versuchsplan mit zwölf experimentellen Durchläufen und drei Zentralpunkten aus. Der Techniker möchte in der Lage sein, einen Effekt von fünf Transparenzeinheiten bei höchstens vier Replikationen zu erkennen. Aus früheren Experimenten ist bekannt, dass 4,5 als ausreichender Schätzwert der Standardabweichung angesehen werden kann. Der Techniker entscheidet, die Trennschärfe für ein Modell mit Haupteffekten und einem Term für Zentralpunkte zu berechnen.
- Wählen Sie aus.
- Geben Sie im Feld Anzahl der Faktoren den Wert 10 ein.
- Wählen Sie im Feld Anzahl der Eckpunkte den Wert 12 aus.
- Geben Sie im Feld Replikationen die Werte 1 2 3 4 ein.
- Geben Sie im Feld Effekte den Wert 5 ein.
- Geben Sie im Feld Anzahl der Zentralpunkte den Wert 3 ein.
- Geben Sie im Feld Standardabweichung den Wert 4,5 ein.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
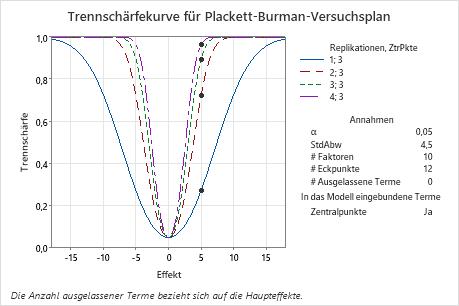
Der Versuchsplan ohne Replikationen weist eine Trennschärfe von ungefähr 30 % auf. Bei einem Versuchsplan mit drei Replikationen und insgesamt 39 Durchläufen wird ein wichtiger Effekt mit einer Wahrscheinlichkeit von nahezu 90 % erkannt. Bei einem Versuchsplan mit vier Replikationen und insgesamt 51 Durchläufen wird ein wichtiger Effekt mit einer Wahrscheinlichkeit von über 95 % erkannt. Die Trennschärfekurve zeigt die Beziehung zwischen der Trennschärfe und der Effektgröße. Die Symbole auf der Kurve stellen die Effektgröße 5 dar, die vom Techniker angegeben wurde. Der Techniker entscheidet, dass der Versuchsplan mit drei Replikationen eine ausreichende Trennschärfe aufweist.
Methode
| Faktoren: | 10 | Versuchsplan: | 12 |
|---|---|---|---|
| Zentralpunkte (gesamt): | 3 |
Ergebnisse
| Zentralpunkte | Effekt | Replikationen | Durchläufe gesamt | Trennschärfe |
|---|---|---|---|---|
| 3 | 5 | 1 | 15 | 0,272032 |
| 3 | 5 | 2 | 27 | 0,720550 |
| 3 | 5 | 3 | 39 | 0,894838 |
| 3 | 5 | 4 | 51 | 0,963485 |
