In diesem Thema
Berechnen der Trennschärfe
Formel
Diese Berechnungen beruhen auf einer F-Verteilung mit dem Nichtzentralitätsparameter λ.
Nichtzentralitätsparameter
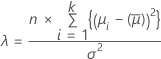
Leistung
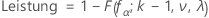
Minitab berechnet λ unter der Annahme des ungünstigsten Falls, dass sämtliche anderen Mittelwerte in der Mitte zwischen Minimum und Maximum liegen. Das Ergebnis ist eine Aufstellung der Mittelwerte, die die Trennschärfe für einen bestimmten Stichprobenumfang und eine bestimmte maximale Differenz zwischen den Mittelwerten minimiert.
Notation
| Begriff | Beschreibung |
|---|---|
| k | Anzahl der Stufen |
| n | Stichprobenumfang auf jeder Stufe |
| α | Signifikanzniveau |
| σ | Standardabweichung |
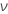 | Freiheitsgrade für Fehler gleich k * (n – 1) |
| fα | kritischer Wert (oberer α-Punkt der F-Verteilung mit k – 1 und ν Freiheitsgraden) |
| μi | Mittelwert der Antwortvariablen auf Stufe i |
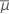 | 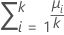 Summe (μi) / k Summe (μi) / k |
 | CDF der F-Verteilung mit k – 1 Freiheitsgraden des Zählers, v Freiheitsgraden des Nenners und Nichtzentralitätsparameter λ, ausgewertet bei fα |
Berechnen des Stichprobenumfangs und der maximalen Differenz
Formel
Wenn Sie Werte für Trennschärfe und Differenz angeben, berechnet Minitab den Wert der maximalen Differenz. Wenn Sie Werte für Trennschärfe und maximale Differenz angeben, berechnet Minitab den Wert des Stichprobenumfangs.
Für diese beiden Fälle verwendet Minitab einen iterativen Algorithmus mit der Trennschärfegleichung. Bei jeder Iteration wertet Minitab die Trennschärfe für einen Versuchsstichprobenumfang oder eine Versuchsdifferenz aus; bei Erreichen der angegebenen Werte wird die Berechnungsprozedur beendet.
Soll-Trennschärfe und Ist-Trennschärfe
Beim Berechnen des Stichprobenumfangs ermittelt Minitab möglicherweise, dass die Soll-Trennschärfe nicht mit einem ganzzahligen Wert für den Stichprobenumfang erreicht wird. In diesem Fall zeigt Minitab den Sollwert für die Trennschärfe neben der tatsächlichen Trennschärfe an. Die Ist-Trennschärfe ist ein Wert, der einem ganzzahligen Stichprobenumfang entspricht und dem Sollwert am nächsten kommt, jedoch größer als dieser ist.
