Schritt 1: Berechnete Werte untersuchen
Anhand der eingegebenen Werte für die zwei Variablen der Trennschärfefunktion berechnet Minitab die Differenz, den Stichprobenumfang oder die Trennschärfe des Tests.
- Maximale Differenz
-
Wenn Sie den Stichprobenumfang und die Trennschärfe eingegeben haben, berechnet Minitab die kleinste Differenz, die mit ausreichender Trennschärfe erkannt werden kann. Diese Differenz ist die Differenz zwischen dem kleinsten Mittelwert und dem größten Mittelwert für die untersuchten Grundgesamtheiten. Wenn ein Forscher beispielsweise die Härte von vier verschiedenen Lackmischungen testen möchte, gibt eine maximale Differenz von 4 an, dass mit dem Test bei ausreichender Trennschärfe eine Differenz zwischen der weichsten und der härtesten Mischung von mindestens 4 erkannt werden kann.
Bei größeren Stichprobenumfängen können mit dem Test kleinere Differenzen erkannt werden. Sie möchten die kleinste Differenz erkennen, die praktische Konsequenzen für Ihre Anwendung hat.
- Stichprobenumfang
-
Wenn Sie die Trennschärfe und die maximale Differenz eingeben, berechnet Minitab den erforderlichen Stichprobenumfang. Der Stichprobenumfang ist die Anzahl der Beobachtungen in jeder Gruppe. Da der Stichprobenumfang als ganze Zahl angegeben wird, kann die tatsächliche Trennschärfe des Tests etwas höher als der von Ihnen angegebene Trennschärfewert ausfallen.
Wenn Sie den Stichprobenumfang vergrößern, nimmt auch die Trennschärfe des Tests zu. Es empfiehlt sich, dass eine ausreichende Anzahl von Beobachtungen in der Stichprobe vorliegen, um eine angemessene Trennschärfe zu erzielen. Der Stichprobenumfang sollte jedoch nicht so groß sein, dass Zeit und Geld bei der Stichprobennahme vergeudet oder irrelevante Differenzen als statistisch signifikant erkannt werden.
- Trennschärfe
-
Wenn Sie die maximale Differenz und den Stichprobenumfang eingegeben haben, berechnet Minitab die Trennschärfe des Tests. Ein Trennschärfewert von 0,9 wird im Allgemeinen als geeignet angesehen. Ein Wert von 0,9 bedeutet, dass eine Differenz zwischen mindestens zwei Mittelwerten mit einer Wahrscheinlichkeit von 90 % erkannt wird, wenn eine solche Differenz in den Grundgesamtheiten tatsächlich vorhanden ist. Bei einem Test mit geringer Trennschärfe erkennen Sie möglicherweise eine Differenz nicht und schließen dann fälschlicherweise, dass keine Differenz vorhanden ist. In der Regel weist der Test bei einem kleineren Stichprobenumfang oder einer kleineren Differenz eine geringere Trennschärfe zum Erkennen einer Differenz auf.
Ergebnisse
| Maximale Differenz | Stichprobenumfang | Trennschärfe |
|---|---|---|
| 4 | 5 | 0,826860 |
Wichtigste Ergebnisse: Maximale Differenz, Stichprobenumfang, Trennschärfe
In diesen Ergebnissen berechnet Minitab für den Stichprobenumfang 5 in jeder der vier Gruppen und für eine maximale Differenz von 4, dass die Trennschärfe des Tests zum Erkennen einer Differenz zwischen dem kleinsten Mittelwert und dem größten Mittelwert ungefähr 0,83 beträgt. Anhand der Trennschärfekurve können Sie auch feststellen, bei welchem größeren Wert für die maximale Differenz der Test beim angegebenen Stichprobenumfang eine Trennschärfe von 0,9 erreicht.
Schritt 2: Trennschärfekurve untersuchen
Mit der Trennschärfekurve können Sie den geeigneten Stichprobenumfang oder die angemessene Trennschärfe für einen Test ermitteln.
Die Trennschärfekurve stellt jede Kombination von Trennschärfe und maximaler Differenz (Differenz zwischen dem kleinsten Mittelwert und dem größten Mittelwert) dar, wenn Stichprobenumfang, Signifikanzniveau, Standardabweichung und Anzahl der Stufen konstant gehalten werden. Jedes Symbol auf der Trennschärfekurve stellt einen Wert dar, der auf der Grundlage der Werte berechnet wurde, die Sie für zwei Eigenschaften eingegeben haben. Wenn Sie beispielsweise einen Stichprobenumfang und eine maximale Differenz eingegeben haben, berechnet Minitab die entsprechende Trennschärfe und zeigt den berechneten Wert in der Grafik an.
Untersuchen Sie die Werte auf der Kurve, um die maximale Differenz zu bestimmen, die der Test bei einer bestimmten Trennschärfe und einem bestimmten Stichprobenumfang erkennen kann. Ein Trennschärfewert von 0,9 wird im Allgemeinen als geeignet angesehen. Einige Fachleute hingegen erachten einen Trennschärfewert von 0,8 als geeignet. Falls eine einfache ANOVA eine zu geringe Trennschärfe aufweist, kann eine Differenz zwischen dem kleinsten Mittelwert und dem größten Mittelwert möglicherweise nicht erkannt werden, auch wenn tatsächlich eine Differenz vorliegt.
Je größer die Differenz, die Sie erkennen möchten, desto größer ist die dafür verfügbare Trennschärfe. Nach Möglichkeit soll die kleinste Differenz erkannt werden, die praktische Auswirkungen hat. Wenn Sie den Stichprobenumfang vergrößern, nimmt auch die Trennschärfe des Tests zu. Es empfiehlt sich, dass eine ausreichende Anzahl von Beobachtungen in der Stichprobe vorliegen, um eine angemessene Trennschärfe zu erzielen. Der Stichprobenumfang sollte jedoch nicht so groß sein, dass Zeit und Geld bei der Stichprobennahme vergeudet oder irrelevante Differenzen als statistisch signifikant erkannt werden.
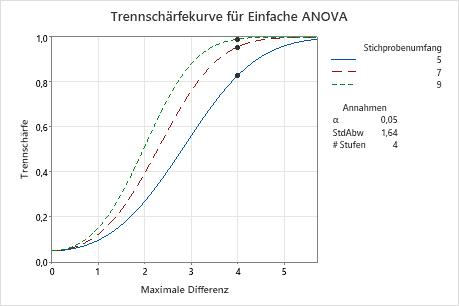
In dieser Grafik ist für jeden Stichprobenumfang eine eigene Kurve vorhanden. Die Trennschärfekurve für einen Stichprobenumfang von 5 in jeder Gruppe zeigt, dass der Test für eine maximale Differenz von 4 eine Trennschärfe von ungefähr 0,8 aufweist. Die Trennschärfekurve für einen Stichprobenumfang von 7 zeigt, dass der Test für eine maximale Differenz von 4 eine Trennschärfe von ungefähr 0,95 aufweist. Die Trennschärfekurve für einen Stichprobenumfang von 9 zeigt, dass der Test für eine maximale Differenz von 4 eine Trennschärfe von annähernd 1,0 aufweist. Bei jeder Kurve für einen Stichprobenumfang nimmt mit zunehmender maximaler Differenz auch die Trennschärfe zu.
