In diesem Thema
Alpha-Niveau
Das Signifikanzniveau (als Alpha oder α bezeichnet) ist das maximal akzeptable Risiko, dass die Nullhypothese zurückgewiesen wird, wenn sie tatsächlich wahr ist (Fehler 1. Art). Wenn Sie beispielsweise eine einfache ANOVA mit den Standardhypothesen durchführen, gibt ein α von 0,05 ein Risiko von 5 % an, dass auf das Vorhandensein einer Differenz geschlossen wird, wenn tatsächlich keine Differenz vorhanden ist.
Interpretation
Verwenden Sie das Signifikanzniveau, um den Trennschärfewert des Tests zu minimieren, wenn die Nullhypothese (H0) wahr ist. Bei höheren Signifikanzniveaus ist der Test trennschärfer, gleichzeitig steigt jedoch die Wahrscheinlichkeit, dass ein Fehler 1. Art auftritt, beim dem die Nullhypothese zurückgewiesen wird, wenn diese tatsächlich wahr ist.
Angenommene Standardabweichung
Die Standardabweichung ist das am häufigsten verwendete Maß für die Streuung bzw. die Streubreite der Daten um den Mittelwert. Eine zufällige oder natürliche Streuung eines Prozesses wird häufig auch als Rauschen bezeichnet.
Interpretation
Die angenommene Standardabweichung ist ein Planschätzwert der Standardabweichung der Grundgesamtheit, die Sie für die Analyse der Trennschärfe eingeben. Minitab verwendet die angenommene Standardabweichung, um die Trennschärfe des Tests zu berechnen. Höhere Werte der Standardabweichung verweisen auf eine stärkere Streuung der Daten, was die statistische Trennschärfe des Tests reduziert.Maximale Differenz
Die maximale Differenz ist die Differenz zwischen dem kleinsten Gruppenmittelwert und dem größten Gruppenmittelwert.
Interpretation
Wenn Sie den Stichprobenumfang und die Trennschärfe eingeben, berechnet Minitab die maximale Differenz. Im Allgemeinen führen größere Stichprobenumfänge dazu, dass bei einer bestimmten Trennschärfe kleinere maximale Differenzen erkannt werden können.
- Bei fünf Beobachtungen pro Gruppe ist die Trennschärfe des Tests 0,9, wenn die Differenz ungefähr 4,4 beträgt.
- Bei sieben Beobachtungen pro Gruppe ist die Trennschärfe des Tests 0,9, wenn die Differenz ungefähr 3,6 beträgt.
- Bei neun Beobachtungen pro Gruppe ist die Trennschärfe des Tests 0,9, wenn die Differenz ungefähr 3,1 beträgt.
Wenn Sie die Beziehung zwischen dem Stichprobenumfang und der erkennbaren Differenz eingehender untersuchen möchten, verwenden Sie die Trennschärfekurve.
Ergebnisse
| Stichprobenumfang | Trennschärfe | Maximale Differenz |
|---|---|---|
| 5 | 0,9 | 4,42404 |
| 7 | 0,9 | 3,58435 |
| 9 | 0,9 | 3,09574 |
Trennschärfe
Die Trennschärfe einer einfachen ANOVA ist die Wahrscheinlichkeit, dass mit dem Test festgestellt wird, dass die maximale Differenz zwischen Gruppenmittelwerten statistisch signifikant ist, wenn diese Differenz tatsächlich vorliegt.
Interpretation
Wenn Sie die maximale Differenz und den Stichprobenumfang eingegeben haben, berechnet Minitab die Trennschärfe des Tests. Ein Trennschärfewert von 0,9 wird im Allgemeinen als geeignet angesehen. Ein Wert von 0,9 bedeutet, dass eine Differenz zwischen mindestens zwei Mittelwerten mit einer Wahrscheinlichkeit von 90 % erkannt wird, wenn eine solche Differenz in den Grundgesamtheiten tatsächlich vorhanden ist. Bei einem Test mit geringer Trennschärfe erkennen Sie möglicherweise eine Differenz nicht und schließen dann fälschlicherweise, dass keine Differenz vorhanden ist. In der Regel weist der Test bei einem kleineren Stichprobenumfang oder einer kleineren Differenz eine geringere Trennschärfe zum Erkennen einer Differenz auf.
In den folgenden Ergebnisse ergibt ein Stichprobenumfang von 4 beispielsweise eine Trennschärfe von ungefähr 0,9 für eine maximale Differenz von 6, jedoch lediglich 0,69 für eine maximale Differenz von 4. Bei jedem Wert der maximalen Differenz steigt beim Vergrößern des Stichprobenumfangs die Trennschärfe des Tests.
Ergebnisse
| Maximale Differenz | Stichprobenumfang | Trennschärfe |
|---|---|---|
| 2 | 4 | 0,206970 |
| 2 | 6 | 0,332203 |
| 2 | 8 | 0,454971 |
| 4 | 4 | 0,688630 |
| 4 | 6 | 0,909626 |
| 4 | 8 | 0,978713 |
| 6 | 4 | 0,968086 |
| 6 | 6 | 0,999226 |
| 6 | 8 | 0,999988 |
Trennschärfekurve
Die Trennschärfekurve zeigt die Trennschärfe des Tests im Vergleich zur maximalen Differenz zwischen dem kleinsten Mittelwert und dem größten Mittelwert.
Interpretation
Mit der Trennschärfekurve können Sie den geeigneten Stichprobenumfang oder die angemessene Trennschärfe für einen Test ermitteln.
Die Trennschärfekurve stellt jede Kombination von Trennschärfe und maximaler Differenz für jeden Stichprobenumfang dar, wenn das Signifikanzniveau und die Standardabweichung konstant gehalten werden. Jedes Symbol auf der Trennschärfekurve stellt einen Wert dar, der auf der Grundlage der Werte berechnet wurde, die Sie für zwei Eigenschaften eingegeben haben. Wenn Sie beispielsweise einen Wert für den Stichprobenumfang und einen Wert für die Trennschärfe eingeben, berechnet Minitab die entsprechende maximale Differenz und zeigt den berechneten Wert wird in der Grafik an.
Untersuchen Sie die Werte auf der Kurve, um die maximale Differenz zu bestimmen, die der Test bei einer bestimmten Trennschärfe und einem bestimmten Stichprobenumfang erkennen kann. Ein Trennschärfewert von 0,9 wird im Allgemeinen als geeignet angesehen. Einige Fachleute hingegen erachten einen Trennschärfewert von 0,8 als geeignet. Falls eine einfache ANOVA eine zu geringe Trennschärfe aufweist, kann eine Differenz zwischen dem kleinsten Mittelwert und dem größten Mittelwert möglicherweise nicht erkannt werden, auch wenn tatsächlich eine Differenz vorliegt.
Wenn Sie den Stichprobenumfang vergrößern, nimmt auch die Trennschärfe des Tests zu. Es empfiehlt sich, dass eine ausreichende Anzahl von Beobachtungen in der Stichprobe vorliegen, um eine angemessene Trennschärfe zu erzielen. Der Stichprobenumfang sollte jedoch nicht so groß sein, dass Zeit und Geld bei der Stichprobennahme vergeudet oder irrelevante Differenzen als statistisch signifikant erkannt werden.
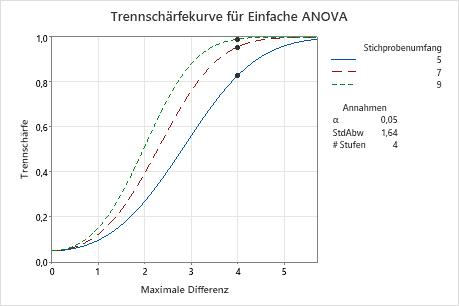
In dieser Grafik ist für jeden Stichprobenumfang eine eigene Kurve vorhanden. Die Trennschärfe für einen Stichprobenumfang von 5 (in jeder Gruppe) zeigt, dass der Test für eine maximale Differenz von 4 eine Trennschärfe von ca. 0,8 aufweist. Die Trennschärfekurve für einen Stichprobenumfang von 7 zeigt, dass der Test für eine maximale Differenz von 4 eine Trennschärfe von ca. 0,95 aufweist. Die Trennschärfekurve für einen Stichprobenumfang von 9 zeigt, dass der Test für eine maximale Differenz von 4 eine Trennschärfe von annähernd 1,0 aufweist. Bei jeder Kurve für einen Stichprobenumfang nimmt mit zunehmender maximaler Differenz auch die Trennschärfe zu.
Stichprobenumfang
Der Stichprobenumfang gibt die Gesamtzahl der Beobachtungen in der Stichprobe an.
Interpretation
Wenn Sie die Trennschärfe und die maximale Differenz eingeben, berechnet Minitab den erforderlichen Stichprobenumfang. Der Stichprobenumfang ist die Anzahl der Beobachtungen in jeder Gruppe. Da der Stichprobenumfang als ganze Zahl angegeben wird, kann die tatsächliche Trennschärfe des Tests etwas höher als der von Ihnen angegebene Trennschärfewert ausfallen.
Wenn Sie den Stichprobenumfang vergrößern, nimmt auch die Trennschärfe des Tests zu. Es empfiehlt sich, dass eine ausreichende Anzahl von Beobachtungen in der Stichprobe vorliegen, um eine angemessene Trennschärfe zu erzielen. Der Stichprobenumfang sollte jedoch nicht so groß sein, dass Zeit und Geld bei der Stichprobennahme vergeudet oder irrelevante Differenzen als statistisch signifikant erkannt werden.
Die folgenden Ergebnisse zeigen beispielsweise, dass für eine maximale Differenz von 4 ein größerer Stichprobenumfang eine größere Trennschärfe ergibt. Ein Stichprobenumfang von 5 in jeder Gruppe liefert eine tatsächliche Trennschärfe von ca. 0,83, während bei einem Stichprobenumfang von 6 eine tatsächliche Trennschärfe von ca. 0,91 erreicht wird.
Ergebnisse
| Maximale Differenz | Stichprobenumfang | Soll-Trennschärfe | Ist-Trennschärfe |
|---|---|---|---|
| 4 | 5 | 0,8 | 0,826860 |
| 4 | 6 | 0,9 | 0,909626 |
