In diesem Thema
Signifikanzniveau (α)
Das Signifikanzniveau (als Alpha oder α bezeichnet) ist der maximal akzeptable Risikograd für einen Fehler 1. Art.
Interpretation
Entscheiden Sie anhand des Signifikanzniveaus, ob eine Differenz statistisch signifikant ist. Da das Signifikanzniveau den Schwellenwert für die statistische Signifikanz darstellt, nimmt mit einem höheren Wert die Wahrscheinlichkeit zu, dass ein Fehler 1. Art auftritt. Ein Fehler 1. Art ist die unzutreffende Schlussfolgerung, dass eine Differenz zwischen den Mittelwerten der verschiedenen Faktorstufen vorhanden ist.
Angenommene Standardabweichung
Die angenommene Standardabweichung ist die geschätzte Standardabweichung in den Messwerten der Antwortvariablen bei replizierten experimentellen Durchläufen. Wenn Sie in Minitab bereits eine Analyse durchgeführt haben, bei der eine ANOVA-Tabelle erstellt wurde, können Sie die Quadratwurzel des korrigierten Mittels der Quadrate für den Fehler verwenden.
Interpretation
Beschreiben Sie mit Hilfe der angenommenen Standardabweichung, wie variabel die Daten sind. Höhere Werte der angenommenen Standardabweichung verweisen auf eine stärkere Streuung bzw. ein stärkeres „Rauschen“ der Daten, was die statistische Trennschärfe eines Versuchsplans reduziert.
Faktoren
Mit dem Wert wird die Anzahl der Faktoren im Versuchsplan angegeben.
Interpretation
Vergewissern Sie sich anhand der Anzahl der Faktoren, dass der Versuchsplan alle Faktoren enthält, die untersucht werden sollen. Die Faktoren sind die Variablen, die im Experiment gesteuert werden. Faktoren werden auch als unabhängige Variablen, erklärende Variablen und Prädiktorvariablen bezeichnet. Die Faktoren können nur eine begrenzte Anzahl von möglichen Werten annehmen; diese werden als Faktorstufen bezeichnet. Für einen allgemeinen vollfaktoriellen Versuchsplan sind alle Faktoren kategorial.
Angenommen, Sie untersuchen Faktoren, die sich während des Fertigungsprozesses auf die Kunststofffestigkeit auswirken. Sie binden den Faktor „Zusatz“ in das Experiment ein. „Zusatz“ ist eine kategoriale Variable, die entweder vom Typ A oder vom Typ B sein kann.
Anzahl der Stufen
In der Liste wird die Anzahl der Stufen in jedem Faktor angegeben, der im Versuchsplan enthalten ist.
Interpretation
Vergewissern Sie sich anhand der Anzahl der Stufen, dass der Versuchsplan alle Faktoren enthält, die untersucht werden sollen. Angenommen, Sie untersuchen Faktoren, die sich während des Fertigungsprozesses auf die Kunststofffestigkeit auswirken. Sie entscheiden, einen Faktor für einen Zusatz einzubinden. Der Zusatz ist eine kategoriale Variable. Der Zusatz kann entweder vom Typ A oder vom Typ B sein. Die Anzahl der Stufen des Faktors für den Zusatz beträgt 2.
Terme in Modell einbinden bis zur Ordnung
Die Modellordnung ist die Wechselwirkung mit der höchsten Ordnung, anhand derer Minitab die Anzahl der Terme bestimmt.
Interpretation
Prüfen Sie anhand der Modellordnung das Modell, das in der Trennschärfeberechnungen angenommen wird. Wenn beispielsweise eine Wechselwirkung zwischen drei Faktoren untersucht werden soll, kann die Modellordnung 3 oder höher sein.
Je höher die Ordnung, desto mehr Terme sind im Modell enthalten. Modelle mit einer größeren Anzahl von Termen weisen weniger Freiheitsgrade für Fehler auf. Damit verfügen Versuchspläne mit mehr Termen über eine geringere Trennschärfe als Versuchspläne mit einer kleineren Anzahl von Termen, sofern alle übrigen Eigenschaften gleich sind. Wenn Sie Berechnungen ausführen, in der die Modellordnung der Anzahl der Faktoren entspricht, erfordern die Berechnungen mehrere Replikationen.
In diesen Ergebnissen beziehen sich die Trennschärfeberechnungen auf das Modell mit Termen bis zur Ordnung 3. Die Anzahl der Faktoren beträgt ebenfalls 3. Da bei diesem Modell alle Freiheitsgrade aus einer einzigen Replikation des Versuchsplans verwendet werden, berechnet Minitab nicht die Trennschärfe für eine einzige Replikation. Wenn Sie dieselbe Berechnung für Terme bis zur Ordnung 2 durchführen, können Sie die Trennschärfe für eine Replikation berechnen.
Ergebnisse
| Maximale Differenz | Replikationen | Durchläufe gesamt | Trennschärfe |
|---|---|---|---|
| 2 | 3 | 108 | 0,930642 |
| 3 | 3 | 108 | 0,999667 |
Maximale Differenz
Die maximale Differenz ist die Differenz zwischen den Faktorstufen mit dem größten und dem kleinsten Mittelwert, die erkannt werden soll. Bei den Berechnungen wird der Faktor verwendet, der die meisten Stufen aufweist, damit die Berechnungen für andere Faktoren konservativ sind. Minitab berechnet die kleinste Differenz, die mit dem Versuchsplan erkannt werden kann. Weitere Replikationen ermöglichen es, dass mit dem Versuchsplan kleinere Differenzen erkannt werden können. Nach Möglichkeit soll die kleinste Differenz erkannt werden, die praktische Konsequenzen für die jeweilige Anwendung hat.
Interpretation
Bestimmen Sie anhand der maximalen Differenz, welche Differenzen mit dem Versuchsplan erkannt werden. Wenn Sie eine Anzahl von Replikationen und einen Trennschärfewert eingeben, berechnet Minitab die maximale Differenz. Im Allgemeinen können Sie mit einer größeren Anzahl von Replikationen eine kleinere maximale Differenz erkennen. Normalerweise gilt Folgendes: Je mehr Replikationen vorhanden sind, desto kleiner ist maximale Differenz, die mit dem Versuchsplan erkannt werden kann.
In diesen Ergebnissen kann mit dem Versuchsplan mit einer Replikation eine Differenz von ca. 3,8 bei einer Trennschärfe von 90 % erkannt werden. Mit dem Versuchsplan mit drei Replikationen kann bei 90 % Trennschärfe eine kleinere Differenz erkannt werden; sie beträgt etwa 1,9.
Die Ergebnisse veranschaulichen außerdem, dass der Faktor mit den meisten Stufen über vier Stufen verfügt. Die berechnete maximale Differenz ist für den Faktor mit vier Stufen genau. Die maximale Differenz für den Faktor mit vier Stufen ist größer als die maximale Differenz für die beiden Faktoren mit drei Stufen.
Ergebnisse
| Replikationen | Durchläufe gesamt | Trennschärfe | Maximale Differenz |
|---|---|---|---|
| 1 | 36 | 0,9 | 3,77758 |
| 3 | 108 | 0,9 | 1,88781 |
Replikationen
Replikationen sind mehrere experimentelle Durchläufe mit denselben Faktoreinstellungen.
Interpretation
Schätzen Sie anhand der Anzahl der Replikationen, wie viele experimentelle Durchläufe in den Versuchsplan eingebunden werden sollen. Wenn Sie eine Trennschärfe und eine maximale Differenz eingeben, berechnet Minitab die Anzahl der Replikationen. Da die Anzahl der Replikationen als ganze Zahl angegeben wird, kann die tatsächliche Trennschärfe größer als der Sollwert ausfallen. Wenn Sie die Anzahl der Replikationen erhöhen, nimmt auch die Trennschärfe des Versuchsplans zu. Es sollte eine ausreichende Anzahl von Replikationen vorliegen, um eine angemessene Trennschärfe zu erreichen.
Da die Anzahl der Replikationen als ganze Zahl angegeben wird, sind die von Ihnen angegebenen Trennschärfewerte die Sollwerte für die Trennschärfe. Die tatsächlichen Trennschärfewerte beziehen sich auf die Anzahl der Replikationen und die Anzahl der Zentralpunkte im Versuchsplan. Die tatsächlichen Trennschärfewerte sind mindestens genau so groß wie die Soll-Trennschärfewerte.
In diesen Ergebnissen berechnet Minitab die Anzahl der Replikationen, mit der eine Soll-Trennschärfe von 80 % und eine Soll-Trennschärfe von 90 % erreicht wird. Zum Erkennen einer Differenz von 2,0 muss der Versuchsplan drei Replikationen aufweisen, um entweder den Sollwert 80 % oder den Sollwert 90 % zu erreichen. Die Trennschärfe für den Versuchsplan mit zwei Replikationen ist kleiner als die Soll-Trennschärfe von 80 %. Zum Erkennen der kleineren Differenz 1,8 wird mit drei Replikationen eine Trennschärfe über 80 %, jedoch unter 90 % erreicht. Wenn die kleinere Differenz mit einer Trennschärfe von 90 % erkannt werden soll, muss der Versuchsplan vier Replikationen aufweisen. Da die Anzahl der Replikationen als ganze Zahl angegeben werden, sind die tatsächlichen Trennschärfen größer als die Soll-Trennschärfen.
Die Ergebnisse veranschaulichen außerdem, dass der Faktor mit den meisten Stufen über vier Stufen verfügt. Die Ergebnisse sind für den Faktor mit vier Stufen genau. Die Anzahl der Replikationen für die beiden Faktoren mit drei Stufen kann hiervon abweichen, insbesondere dann, wenn die tatsächliche Trennschärfe viel größer als die Soll-Trennschärfe ist.
Ergebnisse
| Maximale Differenz | Replikationen | Durchläufe gesamt | Soll-Trennschärfe | Ist-Trennschärfe |
|---|---|---|---|---|
| 2,0 | 3 | 108 | 0,8 | 0,932615 |
| 2,0 | 3 | 108 | 0,9 | 0,932615 |
| 1,8 | 3 | 108 | 0,8 | 0,867493 |
| 1,8 | 4 | 144 | 0,9 | 0,952918 |
Durchläufe gesamt
Ein experimenteller Durchlauf ist eine Kombination von Faktorstufen, bei der Antwortvariablen gemessen werden. Die Gesamtzahl der Durchläufe gibt an, wie viele Messwerte der Antwortvariablen im Versuchsplan enthalten sind. Mehrere Ausführungen ein- und derselben Kombination von Faktorstufen werden als separate experimentelle Durchläufe angesehen und als Replikationen bezeichnet.
Interpretation
Vergewissern Sie sich anhand von „Durchläufe gesamt“, dass der Versuchsplan einen Umfang aufweist, der zu den verfügbaren Ressourcen passt. Für einen allgemeinen vollfaktoriellen Versuchsplan liefert diese Formel die Gesamtzahl der Durchläufe:

| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Replikationen |
| Li | Anzahl der Stufen im i-ten Faktor |
| k | Anzahl der Faktoren |
In diesen Ergebnissen weist das Experiment einen Faktor mit vier Stufen und zwei Faktoren mit drei Stufen auf. Die Anzahl der Durchläufe in einer einzigen Replikation beträgt 4*3*3 = 36. Mit jeder Replikation wird der Umfang um dieselbe Anzahl von Durchläufen erhöht. Damit beläuft sich die Anzahl der Durchläufe in drei Replikationen eines Versuchsplans mit 36 experimentellen Durchläufen auf 36*3 = 108. Experimente mit einer größeren Anzahl von experimentellen Durchläufen weisen eine höhere Trennschärfe zum Erkennen einer Differenz auf.
Ergebnisse
| Maximale Differenz | Replikationen | Durchläufe gesamt | Trennschärfe |
|---|---|---|---|
| 2,5 | 1 | 36 | 0,539953 |
| 2,5 | 3 | 108 | 0,992993 |
Trennschärfe
Die Trennschärfe eines allgemeinen vollfaktoriellen Versuchsplans ist die Wahrscheinlichkeit, dass der Haupteffekt für den Faktor mit den meisten Stufen statistisch signifikant ist. Die Differenz besteht zwischen dem größten und dem kleinsten Mittelwert der Antwortvariablen für den Faktor mit den meisten Stufen. Trennschärfeberechnungen sind konservativ für Faktoren mit weniger Stufen, die sich im gleichen Versuchsplan befinden.
Interpretation
Bestimmen Sie anhand des Trennschärfewerts die Fähigkeit des Versuchsplans, eine Differenz zu erkennen. Wenn Sie eine Anzahl von Replikationen und eine maximale Differenz eingeben, berechnet Minitab die Trennschärfe des Versuchsplans. Ein Trennschärfewert von 0,9 wird im Allgemeinen als geeignet angesehen. Ein Wert von 0,9 gibt an, dass die Differenz zwischen den Faktorstufen mit einer Wahrscheinlichkeit von 90 % erkannt wird, wenn die Differenz die von Ihnen angegebene Größe aufweist. Im Allgemeinen ist die Trennschärfe bei einer kleineren Anzahl von Replikationen niedriger. Bei einem Versuchsplan mit geringer Trennschärfe wird eine Differenz möglicherweise nicht erkannt und fälschlicherweise geschlussfolgert, dass keine Differenz vorhanden ist.
Diese Ergebnisse veranschaulichen, wie die Trennschärfe bei einer zunehmenden Anzahl von Replikationen ansteigt. Für eine Differenz von 2 beträgt die Trennschärfe des Versuchsplans bei einer Replikation annähernd 0,36. Bei drei Replikationen steigt die Trennschärfe auf etwa 0,93.
In diesen Ergebnissen wird zudem ersichtlich, dass eine Zunahme der Effektgröße zu einer Steigerung der Trennschärfe führt. Für einen Versuchsplan mit einer Replikation und einer Differenz von 2 beträgt die Trennschärfe annähernd 0,36. Für einen Versuchsplan mit einer Replikation und einer Differenz von 3 beträgt die Trennschärfe annähernd 0,71.
Ergebnisse
| Maximale Differenz | Replikationen | Durchläufe gesamt | Trennschärfe |
|---|---|---|---|
| 2 | 1 | 36 | 0,362893 |
| 2 | 3 | 108 | 0,932615 |
| 3 | 1 | 36 | 0,712094 |
| 3 | 3 | 108 | 0,999695 |
Trennschärfekurve
Die Trennschärfekurve zeigt die Trennschärfe des Tests im Vergleich zur maximalen Differenz. Die maximale Differenz bezeichnet die Differenz zwischen dem größten und dem kleinsten Mittelwert des Faktors mit den meisten Stufen. Trennschärfeberechnungen sind konservativ für Faktoren mit weniger Stufen, die sich im gleichen Versuchsplan befinden.
Interpretation
Bestimmen Sie anhand der Trennschärfekurve die geeigneten Eigenschaften für das Design.
Die Trennschärfekurve stellt die Beziehung zwischen Trennschärfe und maximaler Differenz für jede Anzahl von Replikationen dar. Jedes Symbol auf der Trennschärfekurve stellt einen Wert dar, der auf der Grundlage der eingegebenen Eigenschaften berechnet wurde. Wenn Sie beispielsweise eine Anzahl von Replikationen und einen Wert für die Trennschärfe eingeben, berechnet Minitab die maximale Differenz und zeigt den berechneten Wert in der Grafik an.
Untersuchen Sie die Werte auf der Kurve, um die Differenz zwischen dem größten und dem kleinsten Mittelwert für den Faktor mit den meisten Stufen zu bestimmen, die das Experiment bei einer bestimmten Trennschärfe und bei einer bestimmten Anzahl von Replikationen erkennen kann. Ein Trennschärfewert von 0,9 wird im Allgemeinen als geeignet angesehen. Einige Fachleute hingegen erachten einen Trennschärfewert von 0,8 als geeignet. Falls ein Versuchsplan eine zu geringe Trennschärfe aufweist, wird eine praktisch signifikante Differenz möglicherweise nicht erkannt. Durch Erhöhen der Gesamtzahl der experimentellen Durchläufe wird die Trennschärfe des Designs erhöht. Es empfiehlt sich, dass der Versuchsplan eine ausreichende Anzahl von experimentellen Durchläufen enthält, um eine angemessene Trennschärfe zu erzielen. Ein Versuchsplan weist eine höhere Trennschärfe beim Erkennen einer größeren Differenz als beim Erkennen einer kleineren Differenz auf.
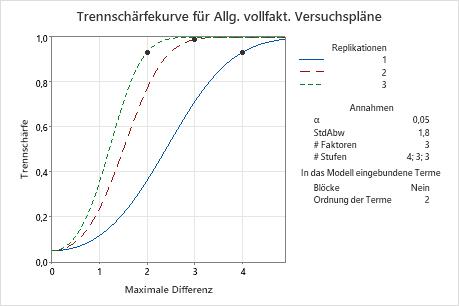
In diesen Ergebnissen berechnet Minitab die Anzahl der Replikationen, mit der eine Trennschärfe von mindestens 0,9 für die maximalen Differenzen 2, 3 oder 4 erreicht wird. Das Diagramm weist für jede Anzahl von Replikationen eine Kurve auf. Zum Erkennen einer maximalen Differenz von 2 bei einer Trennschärfe von mindestens 0,9 sind im Versuchsplan drei Replikationen erforderlich. Das Diagramm enthält eine Kurve für drei Replikationen, und es wird ein Symbol bei der maximalen Differenz von 2 angezeigt, bei der die Trennschärfe 0,9 überschreitet. Damit eine maximale Differenz von 3 bei einer Trennschärfe von mindestens 0,9 erkannt werden kann, müssen im Versuchsplan zwei Replikationen vorhanden sein. Für eine maximale Differenz von 4 bei einer Trennschärfe von mindestens 0,9 benötigt der Versuchsplan eine Replikation.
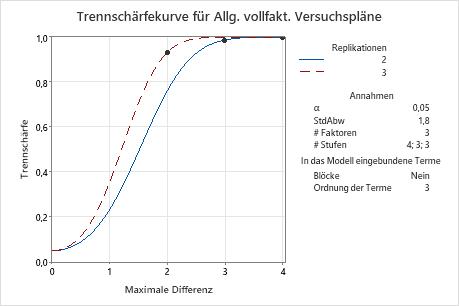
Vergleichen Sie die Trennschärfekurve für eine Ordnung der Terme von 3 mit der Trennschärfekurve für eine Ordnung der Terme von 2. Die Lösung mit einer Replikation ist nur möglich, wenn die Ordnung der Terme kleiner als die Anzahl der Faktoren ist. Wenn die Anzahl der Faktoren gleich der Ordnung der Terme ist, verfügt ein Design mit einer Replikation nicht über ausreichende Freiheitsgrade für Trennschärfeberechnungen. In den Ergebnissen ist die Ordnung der Terme gleich 3, während die Anzahl der Faktoren 3 beträgt, so dass das Design mit einer Replikation keine mögliche Lösung ist. Die Lösung, in der die maximale Differenz 4 beträgt, ist das Design mit zwei Replikationen.
