In diesem Thema
Signifikanzniveau (α)
Das Signifikanzniveau (als Alpha oder α bezeichnet) ist der maximal akzeptable Risikograd für einen Fehler 1. Art.
Interpretation
Entscheiden Sie anhand des Signifikanzniveaus, ob ein Effekt statistisch signifikant ist. Da das Signifikanzniveau den Schwellenwert für die statistische Signifikanz darstellt, nimmt mit einem höheren Wert die Wahrscheinlichkeit zu, dass ein Fehler 1. Art auftritt. Ein Fehler 1. Art ist die unzutreffende Schlussfolgerung, dass ein Effekt statistisch signifikant ist.
Angenommene Standardabweichung
Die angenommene Standardabweichung ist die geschätzte Standardabweichung in den Messwerten der Antwortvariablen bei replizierten experimentellen Durchläufen. Wenn Sie in Minitab bereits eine Analyse durchgeführt haben, bei der eine ANOVA-Tabelle erstellt wurde, können Sie die Quadratwurzel des korrigierten Mittels der Quadrate für den Fehler verwenden.
Interpretation
Beschreiben Sie mit Hilfe der angenommenen Standardabweichung, wie variabel die Daten sind. Höhere Werte der angenommenen Standardabweichung verweisen auf eine stärkere Streuung bzw. ein stärkeres „Rauschen“ der Daten, was die statistische Trennschärfe eines Versuchsplans reduziert.
Faktoren
Mit dem Wert wird die Anzahl der Faktoren im Design angegeben.
Interpretation
Vergewissern Sie sich anhand der Anzahl der Faktoren, dass der Versuchsplan alle Faktoren enthält, die untersucht werden sollen. Die Faktoren sind die Variablen, die im Experiment gesteuert werden. Faktoren werden auch als unabhängige Variablen, erklärende Variablen und Prädiktorvariablen bezeichnet. Für die Berechnungen von Trennschärfe und Stichprobenumfang sind alle Faktoren numerisch. Für numerische Faktoren werden nur wenige kontrollierte Werte im Experiment genutzt, selbst wenn diese viele Werte annehmen können. Diese Werte werden als Faktorstufen bezeichnet.
Angenommen, Sie untersuchen Faktoren, die sich während des Fertigungsprozesses auf die Kunststofffestigkeit auswirken. Sie binden „Temperatur“ in das Experiment ein. Da es sich bei „Temperatur“ um einen Faktor handelt, enthält das Experiment lediglich drei Temperatureinstellungen: 100 °C, 150 °C und 200 °C.
Basisversuchsplan
Die Zahlen geben die Anzahl der Faktoren sowie die Anzahl der Eckpunkte im Basisversuchsplan an.
Interpretation
Bestimmen Sie anhand des Basisversuchsplans, ob es sich bei dem Versuchsplan um einen teilfaktoriellen oder einen teilfaktoriellen Versuchsplan handelt. Wenn die Anzahl der Eckpunkte kleiner als 2^(Anzahl der Faktoren) ist, handelt es sich beim Versuchsplan um einen teilfaktoriellen Versuchsplan. In einem teilfaktoriellen Versuchsplan sind nicht alle Terme, die mit dem Versuchsplan geschätzt werden können, unabhängig voneinander. Um festzustellen, wie die Terme voneinander abhängen, erstellen Sie den Versuchsplan, und untersuchen Sie die Aliastabelle.
Der Basisversuchsplan stellt den Ausgangspunkt dar, von dem aus Sie Ihren endgültigen Versuchsplan entwickeln können. Sie können dem Basisversuchsplan zu verschiedenen Zwecken Elemente hinzufügen. Sie können beispielsweise Replikationen oder Zentralpunkte hinzufügen, um die Trennschärfe des Versuchsplans zu erhöhen.
Blöcke
Mit dem Wert wird die Anzahl der Blöcke im Versuchsplan angegeben.
Interpretation
Ermitteln Sie anhand der Anzahl der Blöcke den Versuchsplan, der für die Trennschärfeberechnungen verwendet wird. Blöcke sind Gruppen von Durchläufen eines Experiments, die unter relativ homogenen Bedingungen ausgeführt werden. Obwohl jede Messung unter gleichen experimentellen Bedingungen erfolgen sollte (ausgenommen diejenigen, die als Teil des Experiments variiert werden), ist dies nicht immer möglich.
Angenommen, Sie möchten die Qualität einer neuen Druckerpresse testen. Die Einrichtung der Presse nimmt jedoch mehrere Stunden in Anspruch und kann nur viermal täglich vorgenommen werden. Da der Versuchsplan für das Experiment mindestens acht Durchläufe erfordert, benötigen Sie für den Test der Presse mindestens zwei Tage. Die von Tag zu Tag eventuell unterschiedlichen Bedingungen können Sie durch Verwendung von „Tag“ als Variable zur Blockbildung erklären. Um zwischen einem Blockeffekt (zufällige Unterschiede zwischen den Tagen) und Effekten durch experimentelle Faktoren (Temperatur, Feuchtigkeit und Bediener der Presse) unterscheiden zu können, müssen Sie den Block (Tag) im Versuchsplan erklären. Die Durchlaufreihenfolge innerhalb der Blöcke sollte randomisiert werden. Weitere Informationen dazu, wie Minitab Durchläufe zu Blöcken zuordnet, finden Sie unter Was ist ein Block?
Zentralpunkte pro Block
Mit dem Wert wird die Anzahl der Zentralpunkte pro Block im Versuchsplan angegeben.
Interpretation
Ermitteln Sie anhand der Anzahl der Zentralpunkte pro Block den Versuchsplan, der für die Trennschärfeberechnungen verwendet wird. Zentralpunkte sind Durchläufe, bei denen alle Faktorstufen auf die Mitte zwischen ihrer hohen und ihrer niedrigen Stufe festgelegt sind. Wenn der Versuchsplan Blöcke enthält, fügt Minitab jedem Block die gleiche Anzahl von Zentralpunkten hinzu. Wenn Sie beispielsweise zwei Zentralpunkte pro Block und zwei Blöcke angeben, enthält der Versuchsplan vier Zentralpunkte.
Zentralpunkte haben in der Regel nur einen geringen Einfluss auf die Ergebnisse, wenn der Versuchsplan Replikationen der Eckpunkte enthält. Zentralpunkte finden neben ihrem Einfluss auf die Berechnungen der Trennschärfe weitere Anwendung. So sind Zentralpunkte beispielsweise beim Test auf Krümmung in der Antwortvariablen erforderlich.
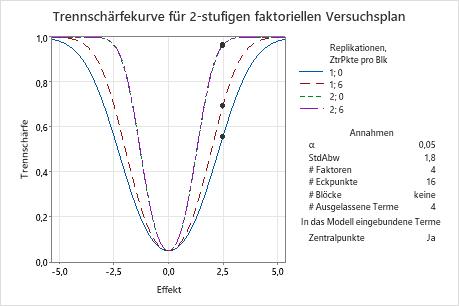
In diesen Ergebnissen stellen die Punkte auf den Trennschärfekurven Berechnungen für eine Differenz von 2,5 dar. Der Versuchsplan mit einer Replikation und ohne Zentralpunkte weist eine Trennschärfe von annähernd 0,56 auf. Der Versuchsplan mit einer Replikation und sechs Zentralpunkten verfügt über eine Trennschärfe von fast 0,7. Bei zwei Replikationen sind die Trennschärfekurven für null Zentralpunkte und sechs Zentralpunkte in der Grafik nicht voneinander zu unterscheiden. Die Kurve für sechs Zentralpunkte liegt für Effekte ungleich null etwas höher. Beide Trennschärfewerte liegen über 0,95.
Methode
| Faktoren: | 4 | Basisversuchsplan: | 4; 16 |
|---|---|---|---|
| Blöcke: | keine |
Ergebnisse
| Zentralpunkte | Effekt | Replikationen | Durchläufe gesamt | Trennschärfe |
|---|---|---|---|---|
| 0 | 2,5 | 1 | 16 | 0,557255 |
| 0 | 2,5 | 2 | 32 | 0,961939 |
| 6 | 2,5 | 1 | 22 | 0,696490 |
| 6 | 2,5 | 2 | 38 | 0,965121 |
Effekt
Wenn Sie die Anzahl der Replikationen, den Wert für die Trennschärfe und die Anzahl der Zentralpunkte eingeben, berechnet Minitab den Effekt. Der Effekt ist die Differenz in den Werten der Antwortvariablen zwischen der hohen und der tiefen Stufe eines Faktors, die mit dem Versuchsplan erkannt werden soll. Diese Differenz ist auf nur einen Faktor (Haupteffekt) zurückzuführen.
Interpretation
Bestimmen Sie anhand der Effektgröße, ob mit dem Versuchsplan ein Effekt erkannt werden kann. Wenn Sie eine Anzahl von Replikationen, eine Trennschärfe und eine Anzahl von Zentralpunkten eingeben, berechnet Minitab die kleinste Effektgröße, die mit dem Versuchsplan mit der angegebenen Trennschärfe erkannt werden kann. Im Allgemeinen können bei einer größeren Anzahl von Replikationen in einem Versuchsplan kleinere Effekte erkannt werden.
In diesen Ergebnissen kann mit dem Versuchsplan mit einer Replikation eine Differenz von ca. 0,015 bei einer Trennschärfe von 80 % erkannt werden. Die Differenz, die mit dem Versuchsplan bei einer Trennschärfe von 90 % erkannt werden kann, ist größer als 0,015 und beträgt annähernd 0,018. Mit dem Versuchsplan mit zwei Replikationen kann bei 80 % Trennschärfe eine kleinere Differenz als 0,015 erkannt werden; sie beträgt etwa 0,007.
Methode
| Faktoren: | 5 | Basisversuchsplan: | 5; 32 |
|---|---|---|---|
| Blöcke: | keine |
Ergebnisse
| Zentralpunkte | Replikationen | Durchläufe gesamt | Trennschärfe | Effekt |
|---|---|---|---|---|
| 4 | 1 | 36 | 0,8 | 0,0153027 |
| 4 | 1 | 36 | 0,9 | 0,0180278 |
| 4 | 2 | 68 | 0,8 | 0,0073261 |
| 4 | 2 | 68 | 0,9 | 0,0084775 |
Replikationen
Replikationen sind mehrere experimentelle Durchläufe mit denselben Faktoreinstellungen.
Interpretation
Schätzen Sie anhand der Anzahl der Replikationen, wie viele experimentelle Durchläufe in den Versuchsplan eingebunden werden sollen. Wenn Sie eine Trennschärfe, eine Effektgröße und die Anzahl der Zentralpunkte eingeben, berechnet Minitab die Anzahl der Replikationen. Da die Anzahl der Replikationen und die Anzahl der Zentralpunkt als ganze Zahlen angegeben werden, kann die tatsächliche Trennschärfe größer als der Sollwert ausfallen. Wenn Sie die Anzahl der Replikationen erhöhen, nimmt auch die Trennschärfe des Versuchsplans zu. Es sollte eine ausreichende Anzahl von Replikationen vorliegen, um eine angemessene Trennschärfe zu erreichen.
Da die Anzahl der Replikationen als ganze Zahl angegeben wird, sind die von Ihnen angegebenen Trennschärfewerte die Sollwerte für die Trennschärfe. Die tatsächlichen Trennschärfewerte beziehen sich auf die Anzahl der Replikationen und die Anzahl der Zentralpunkte im Versuchsplan. Die tatsächlichen Trennschärfewerte sind mindestens genau so groß wie die Soll-Trennschärfewerte.
In diesen Ergebnissen berechnet Minitab die Anzahl der Replikationen, mit der die Soll-Trennschärfe erreicht wird. Für einen Versuchsplan, mit dem ein Effekt von 2 bei einer Trennschärfe von 0,8 erkannt werden kann, wird eine Replikation benötigt. Um eine Trennschärfe von 0,9 zu erreichen, muss der Versuchsplan zwei Replikationen aufweisen. Die tatsächliche Trennschärfe bei zwei Replikationen ist größer als 0,99. Diese tatsächliche Trennschärfe ist der kleinste Trennschärfewert, der größer oder gleich 0,9 ist und mit einer ganzzahligen Anzahl von Replikationen erreicht werden kann. Um den kleineren Effekt von 0,9 mit einer Trennschärfe von 0,8 erkennen zu können, muss der Versuchsplan vier Replikationen aufweisen. Um den kleineren Effekt von 0,9 mit einer Trennschärfe von 0,9 erkennen zu können, muss der Versuchsplan fünf Replikationen aufweisen.
Methode
| Faktoren: | 15 | Basisversuchsplan: | 15; 32 |
|---|---|---|---|
| Blöcke: | keine |
Ergebnisse
| Zentralpunkte | Effekt | Replikationen | Durchläufe gesamt | Soll-Trennschärfe | Ist-Trennschärfe |
|---|---|---|---|---|---|
| 0 | 2,0 | 1 | 32 | 0,8 | 0,877445 |
| 0 | 2,0 | 2 | 64 | 0,9 | 0,995974 |
| 0 | 0,9 | 4 | 128 | 0,8 | 0,843529 |
| 0 | 0,9 | 5 | 160 | 0,9 | 0,914018 |
Vergleichen Sie die erste Gruppe von Ergebnissen mit der zweiten Gruppe von Ergebnissen. In der ersten Gruppe von Ergebnissen wurden 16 Terme aus dem Modell ausgelassen. In der zweiten Gruppe von Ergebnissen enthält das Modell alle Terme, die geschätzt werden können. Da im zweiten Modell alle Freiheitsgrade für eine einzige Replikation des Versuchsplans verwendet werden, bietet Minitab 1 Replikation nicht als Lösung an. Aufgrund der höheren Anzahl von Termen im Modell sind die anderen Trennschärfewerte niedriger als in den Ergebnissen für das Modell, bei dem Terme ausgelassen wurden. Die tatsächliche Trennschärfe für den Versuchsplan mit fünf Replikationen beträgt z. B. in der ersten Gruppe von Ergebnissen ungefähr 0,9140 und in der zweiten Gruppe von Ergebnissen ungefähr 0,9136.
Methode
| Faktoren: | 15 | Basisversuchsplan: | 15; 32 |
|---|---|---|---|
| Blöcke: | keine |
Ergebnisse
| Zentralpunkte | Effekt | Replikationen | Durchläufe gesamt | Soll-Trennschärfe | Ist-Trennschärfe |
|---|---|---|---|---|---|
| 0 | 2,0 | 2 | 64 | 0,8 | 0,995347 |
| 0 | 2,0 | 2 | 64 | 0,9 | 0,995347 |
| 0 | 0,9 | 4 | 128 | 0,8 | 0,842492 |
| 0 | 0,9 | 5 | 160 | 0,9 | 0,913575 |
Durchläufe gesamt
Ein experimenteller Durchlauf ist eine Kombination von Faktorstufen, bei der Antwortvariablen gemessen werden. Die Gesamtzahl der Durchläufe gibt an, wie viele Messwerte der Antwortvariablen im Versuchsplan enthalten sind. Mehrere Ausführungen ein- und derselben Kombination von Faktorstufen werden als separate experimentelle Durchläufe angesehen und als Replikationen bezeichnet.
Interpretation
Vergewissern Sie sich anhand von „Durchläufe gesamt“, dass der Versuchsplan einen Umfang aufweist, der zu den verfügbaren Ressourcen passt. Für einen 2-stufigen faktoriellen Versuchsplan liefert diese Formel die Gesamtzahl der experimentellen Durchläufe:

| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Replikationen |
| r | Anzahl der Eckpunkte pro Replikation |
| zpblock | Anzahl der Zentralpunkte pro Block |
| b | Anzahl der Blöcke |
In diesen Ergebnissen verfügt der Basisversuchsplan über 16 Eckpunkte. Der Versuchsplan enthält vier Blöcke und vier Zentralpunkte pro Block und somit insgesamt 4*4 = 16 Zentralpunkte. Daher weist der Versuchsplan mit einer Replikation 16 Eckpunkte und 16 Zentralpunkte und damit 16 + 16 = 32 experimentelle Durchläufen auf. Im Versuchsplan mit zwei Replikationen verdoppelt sich die Anzahl der Eckpunkte auf 2*16 = 32. Die Anzahl der Blöcke und die Anzahl der Zentralpunkte pro Block bleibt dabei unverändert. Demzufolge weist der Versuchsplan mit zwei Replikationen eine Gesamtzahl von 32 + 16 = 48 Durchläufen auf.
Methode
| Faktoren: | 4 | Basisversuchsplan: | 4; 16 |
|---|---|---|---|
| Blöcke: | 4 |
Ergebnisse
| Zentralpunkte pro Block | Effekt | Replikationen | Durchläufe gesamt | Trennschärfe |
|---|---|---|---|---|
| 4 | 2,5 | 1 | 32 | 0,741569 |
| 4 | 2,5 | 2 | 48 | 0,967699 |
Trennschärfe
Die Trennschärfe eines Designs ist die Wahrscheinlichkeit, dass mit dem Design ermittelt werden kann, dass ein Effekt statistisch signifikant ist. Die Differenz zwischen den Mittelwerten der Antwortvariablen auf der hohen und niedrigen Stufe eines Faktors ist die Effektgröße.
Interpretation
Verwenden Sie den Trennschärfewert, um zu ermitteln, ob der Versuchsplan die Fähigkeit aufweist, einen Effekt zu erkennen. Wenn Sie die Anzahl von Replikationen, die Effektgröße und die Anzahl von Zentralpunkten eingeben, berechnet Minitab die Trennschärfe des Versuchsplans. Ein Trennschärfewert von 0,9 wird im Allgemeinen als geeignet angesehen. Ein Wert von 0,9 bedeutet, dass mit dem Versuchsplan ein Effekt der von Ihnen angegebenen Größe mit einer Wahrscheinlichkeit von 90 % erkannt wird. In der Regel ist die Trennschärfe umso kleiner, je kleiner die Anzahl der Replikationen ist. Bei einem Versuchsplan mit geringer Trennschärfe erkennen Sie möglicherweise einen Effekt nicht und schließen dann fälschlicherweise, dass kein Effekt vorhanden ist.
Diese Ergebnisse veranschaulichen, wie die Trennschärfe bei einer zunehmenden Anzahl von experimentellen Durchläufen ansteigt. Bei insgesamt 64 Durchläufen und einer Effektgröße von 0,9 beträgt die Trennschärfe ungefähr 0,55. Bei insgesamt 160 Durchläufen erhöht sich die Trennschärfe des Versuchsplans auf ungefähr 0,91.
In diesen Ergebnissen wird zudem ersichtlich, dass eine Zunahme der Effektgröße zu einer Steigerung der Trennschärfe führt. Bei einem Versuchsplan mit 64 Durchläufen und einer Effektgröße von 0,9 beträgt die Trennschärfe ungefähr 0,55. Bei einer Effektgröße von 1,5 steigt die Trennschärfe auf ungefähr 0,93.
Methode
| Faktoren: | 15 | Basisversuchsplan: | 15; 32 |
|---|---|---|---|
| Blöcke: | keine |
Ergebnisse
| Zentralpunkte | Effekt | Replikationen | Durchläufe gesamt | Trennschärfe |
|---|---|---|---|---|
| 0 | 1,5 | 5 | 160 | 0,999830 |
| 0 | 1,5 | 2 | 64 | 0,932932 |
| 0 | 0,9 | 5 | 160 | 0,914018 |
| 0 | 0,9 | 2 | 64 | 0,545887 |
Trennschärfekurve
Die Trennschärfekurve stellt die Trennschärfe des Versuchsplans im Vergleich zur Größe des Effekts dar. Der Effekt bezieht sich auf die Differenz zwischen dem Mittelwert der Antwortvariablen auf der hohen und der niedrigen Stufe eines Faktors.
Interpretation
Bestimmen Sie anhand der Trennschärfekurve die geeigneten Eigenschaften für das Design.
Die Trennschärfekurve stellt die Beziehung zwischen Trennschärfe und Effektgröße für jede Kombination von Zentralpunkten und Replikationen dar. Jedes Symbol auf der Trennschärfekurve stellt einen Wert dar, der auf der Grundlage der eingegebenen Eigenschaften berechnet wurde. Wenn Sie beispielsweise eine Anzahl von Replikationen, einen Wert für die Trennschärfe und eine Anzahl von Zentralpunkten eingeben, berechnet Minitab die entsprechende Effektgröße und zeigt den berechneten Wert für die Kombination von Replikationen und Zentralpunkten in der Grafik an. Wenn Sie die Replikationen oder Zentralpunkte ermitteln, enthält das Diagramm außerdem Kurven für andere Kombinationen von Replikationen und Zentralpunkten, die zu den Kombinationen gehören, mit denen die Soll-Trennschärfe erreicht wird. Im Diagramm werden keine Kurven für Fälle angezeigt, in denen nicht genügend Freiheitsgrade vorliegen, um die statistische Signifikanz auszuwerten.
Untersuchen Sie die Werte auf der Kurve, um die Effektgröße zu bestimmen, die das Experiment bei einer bestimmten Trennschärfe, einer bestimmten Anzahl von Eckpunkten und einer bestimmten Anzahl von Zentralpunkten erkennen kann. Ein Trennschärfewert von 0,9 wird im Allgemeinen als geeignet angesehen. Einige Fachleute hingegen erachten einen Trennschärfewert von 0,8 als geeignet. Falls ein Versuchsplan eine zu geringe Trennschärfe aufweist, wird ein praktisch signifikanter Effekt möglicherweise nicht erkannt. Durch Erhöhen der Anzahl von Replikationen wird die Trennschärfe des Versuchsplans erhöht. Es empfiehlt sich, dass der Versuchsplan eine ausreichende Anzahl von experimentellen Durchläufen enthält, um eine angemessene Trennschärfe zu erzielen. Ein Versuchsplan weist eine höhere Trennschärfe beim Erkennen eines größeren Effekts als beim Erkennen eines kleineren Effekts auf.
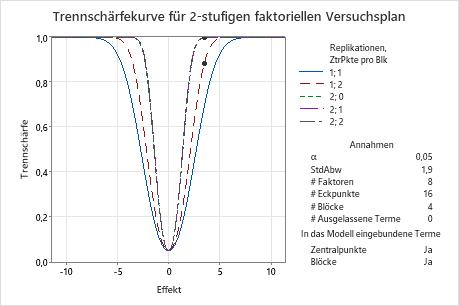
In diesen Ergebnissen berechnet Minitab die Anzahl der Replikationen, mit der für eine Effektgröße von 3,5 eine Soll-Trennschärfe von mindestens 0,8 oder 0,9 erreicht wird. Der Versuchsplan weist 16 Eckpunkte in vier Blöcken auf, damit vier Faktoren untersucht werden können. Bei den Berechnungen werden Versuchspläne mit 0, 1 oder 2 Zentralpunkten pro Block berücksichtigt. Die Kurve, die eine Replikation und zwei Zentralpunkte darstellt, weist ein Symbol für den Effekt von 3,5 auf, bei dem die Trennschärfe höher als die Soll-Trennschärfe von 0,8 liegt. Die drei Kurven, die die Experimente mit zwei Replikationen darstellen, weisen Symbole auf, die zeigen, dass die Trennschärfe zum Erkennen eines Effekts von 3,5 die Soll-Trennschärfe von 0,9 überschreitet.
Da sowohl eine Lösung mit zwei Replikationen und einem Zentralpunkt als auch eine Lösung mit einer Replikation und zwei Zentralpunkten vorhanden ist, enthält das Diagramm außerdem eine Kurve für ein Experiment mit einer Replikation und einem Zentralpunkt. Bei diesem Experiment wird für den Effekt von 3,5 keine der beiden Soll-Trennschärfen erreicht, so dass diese Kurve kein Symbol aufweist. Das Diagramm enthält nicht das Symbol mit einer Replikation und null Zentralpunkten, da dieses Experiment über keine ausreichenden Freiheitsgrade verfügt, um bei Auslassen von null Termen aus dem Modell die statistische Signifikanz auszuwerten.
