α (Alpha)
Das Signifikanzniveau (als α oder Alpha bezeichnet) ist das maximal akzeptable Risiko, dass die Nullhypothese zurückgewiesen wird, wenn sie tatsächlich wahr ist (Fehler 1. Art). Alpha wird auch als Trennschärfe des Tests interpretiert, wenn die Nullhypothese (H0) wahr ist. Im Allgemeinen wählen Sie das Signifikanzniveau aus, bevor Sie die Daten analysieren. Das standardmäßige Signifikanzniveau beträgt 0,05.
Interpretation
Verwenden Sie das Signifikanzniveau, um den Trennschärfewert des Tests zu minimieren, wenn die Nullhypothese (H0) wahr ist. Bei höheren Signifikanzniveaus ist der Test trennschärfer, gleichzeitig steigt jedoch die Wahrscheinlichkeit, dass ein Fehler 1. Art auftritt, beim dem die Nullhypothese zurückgewiesen wird, wenn diese tatsächlich wahr ist.
Vergleichsanteil
Der Vergleichsanteil ist der Anteil, der mit dem Anteil p0 verglichen werden soll.
Interpretation
Minitab berechnet den Vergleichsanteil. Die Differenz zwischen dem Vergleichsanteil und dem Anteil (p0) ist die minimale Differenz, bei der die angegebene Trennschärfe für die einzelnen Stichprobenumfänge erreicht werden kann. Bei größeren Stichprobenumfängen können mit dem Test kleinere Differenzen erkannt werden. Sie möchten die kleinste Differenz erkennen, die praktische Konsequenzen für Ihre Anwendung hat.
Wenn Sie die Beziehung zwischen dem Stichprobenumfang und dem Vergleichsanteil bei einer bestimmten Trennschärfe eingehender untersuchen möchten, verwenden Sie die Trennschärfekurve.
Stichprobenumfang
Der Stichprobenumfang gibt die Gesamtzahl der Beobachtungen in der Stichprobe an.
Interpretation
Anhand des Stichprobenumfangs können Sie schätzen, wie viele Beobachtungen Sie benötigen, um bei einer angegebenen Differenz eine bestimmte Trennschärfe für den Hypothesentest zu erreichen.
Minitab berechnet, wie groß der Stichprobenumfang sein muss, damit in einem Test mit einer bestimmten Trennschärfe die Differenz zwischen dem Anteil und dem Vergleichsanteil erkannt werden kann. Da der Stichprobenumfang als ganze Zahl angegeben wird, kann die tatsächliche Trennschärfe des Tests etwas höher als der von Ihnen angegebene Trennschärfewert ausfallen.
Wenn Sie den Stichprobenumfang vergrößern, nimmt auch die Trennschärfe des Tests zu. Es empfiehlt sich, dass eine ausreichende Anzahl von Beobachtungen in der Stichprobe vorliegen, um eine angemessene Trennschärfe zu erzielen. Der Stichprobenumfang sollte jedoch nicht so groß sein, dass Zeit und Geld bei der Stichprobennahme vergeudet oder irrelevante Differenzen als statistisch signifikant erkannt werden.
Wenn Sie die Beziehung zwischen dem Stichprobenumfang und der Differenz bei einer bestimmten Trennschärfe eingehender untersuchen möchten, verwenden Sie die Trennschärfekurve.
Trennschärfe
Die Trennschärfe eines Hypothesentests ist die Wahrscheinlichkeit, dass die Nullhypothese beim Test zutreffenderweise zurückgewiesen wird. Die Trennschärfe eines Hypothesentests wird vom Stichprobenumfang, der Differenz, der Streuung der Daten und dem Signifikanzniveau des Tests beeinflusst.
Weitere Informationen finden Sie unter Was ist die Trennschärfe?.
Interpretation
Minitab berechnet die Trennschärfe des Tests auf der Grundlage des angegebenen Vergleichsanteils und des angegebenen Stichprobenumfangs. Ein Trennschärfewert von 0,9 wird im Allgemeinen als geeignet angesehen. Ein Wert von 0,9 bedeutet, dass eine Differenz zwischen den Anteilen der Grundgesamtheiten mit einer Wahrscheinlichkeit von 90 % erkannt wird, wenn eine solche Differenz tatsächlich vorhanden ist. Bei einem Test mit geringer Trennschärfe erkennen Sie möglicherweise eine Differenz nicht und schließen dann fälschlicherweise, dass keine Differenz vorhanden ist. In der Regel weist der Test bei einem kleineren Stichprobenumfang oder einer kleineren Differenz eine geringere Trennschärfe zum Erkennen einer Differenz auf.
Wenn Sie einen Vergleichsanteil und einen Trennschärfewert für den Test eingeben, berechnet Minitab, wie groß die Stichprobe sein muss. Minitab berechnet außerdem die tatsächliche Trennschärfe des Tests für diesen Stichprobenumfang. Da der Stichprobenumfang als ganze Zahl angegeben wird, kann die tatsächliche Trennschärfe des Tests etwas höher als der von Ihnen angegebene Trennschärfewert ausfallen.
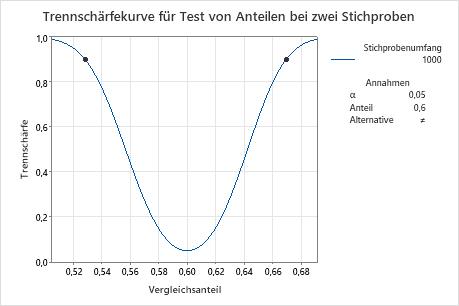
Trennschärfekurve
Die Trennschärfekurve zeigt die Trennschärfe des Tests im Vergleich zum Vergleichsanteil.
Interpretation
Mit der Trennschärfekurve können Sie den geeigneten Stichprobenumfang oder die angemessene Trennschärfe für einen Test ermitteln.
Die Trennschärfekurve stellt jede Kombination von Trennschärfe und Vergleichsanteil für jeden Stichprobenumfang dar, wenn das Signifikanzniveau konstant gehalten wird. Jedes Symbol auf der Trennschärfekurve stellt einen Wert dar, der auf der Grundlage der eingegebenen Werte berechnet wurde. Wenn Sie beispielsweise einen Wert für den Stichprobenumfang und einen Wert für die Trennschärfe eingeben, berechnet Minitab den entsprechenden Vergleichsanteil und zeigt den berechneten Wert in der Grafik an.
Untersuchen Sie die Werte auf der Kurve, um die Differenz zwischen dem Vergleichsanteil und dem Anteil zu bestimmen, die bei einer bestimmten Trennschärfe und einem bestimmten Stichprobenumfang erkannt werden kann. Ein Trennschärfewert von 0,9 wird im Allgemeinen als geeignet angesehen. Einige Fachleute hingegen erachten einen Trennschärfewert von 0,8 als geeignet. Falls ein Hypothesentest eine zu geringe Trennschärfe aufweist, kann eine Differenz mit praktischer Signifikanz möglicherweise nicht erkannt werden. Wenn Sie den Stichprobenumfang vergrößern, nimmt auch die Trennschärfe des Tests zu. Es empfiehlt sich, dass eine ausreichende Anzahl von Beobachtungen in der Stichprobe vorliegen, um eine angemessene Trennschärfe zu erzielen. Der Stichprobenumfang sollte jedoch nicht so groß sein, dass Zeit und Geld bei der Stichprobennahme vergeudet oder irrelevante Differenzen als statistisch signifikant erkannt werden. Wenn Sie die Größe der zu erkennenden Differenz verringern, nimmt damit auch die Trennschärfe ab.
In dieser Grafik veranschaulicht die Trennschärfekurve, dass der Test bei einem Stichprobenumfang von 1000 und einer Trennschärfe von 0,8 eine Differenz zwischen dem Vergleichsanteil und dem Anteil (p0) von annähernd 0,006 in beiden Richtungen erkennen kann. Die Trennschärfekurve zeigt, dass sich die vom Test erkennbare Differenz bei einer Steigerung der Trennschärfe auf 0,9 an 0,007 annähert.