Wählen Sie die gewünschte Methode oder Formel aus.
Berechnen der Trennschärfe
Formel
Einseitige Trennschärfe (H 1: λ > λ 0)
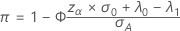
Einseitige Trennschärfe (H 1: λ <λ 0)
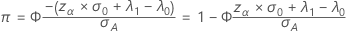
Beidseitige Trennschärfe (H 1: λ ≠ λ 0)
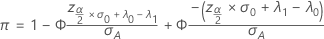
Notation
| Begriff | Beschreibung |
|---|---|
| Φ | kumulative Verteilungsfunktion (CDF) der Standardnormalverteilung |
| zα | Φ-1 (1 - α), wobei Φ-1 die inverse kumulative Verteilungsfunktion der Standardnormalverteilung ist |
| λ | wahrer Wert der Rate der Grundgesamtheit |
| λ 0 | hypothetischer Wert der Rate der Grundgesamtheit |
| λ 1 | Vergleichsrate |
| σ 0 | Standardabweichung gemäß der Nullhypothese, gleich  |
| σ A | Standardabweichung gemäß der Alternativhypothese, gleich  |
Berechnen des Stichprobenumfangs und der Vergleichsrate
Wenn Sie Werte für die Trennschärfe und den Stichprobenumfang angeben, berechnet Minitab den Wert der Vergleichsrate. Wenn Sie Werte für die Trennschärfe und die Vergleichsrate angeben, berechnet Minitab den Wert des Stichprobenumfangs.
Für diese beiden Fälle verwendet Minitab einen iterativen Algorithmus zum Ermitteln des optimalen Werts. Bei jeder Iteration wertet Minitab die Trennschärfe für einen Versuchsstichprobenumfang oder eine Versuchsvergleichsrate aus; wenn die Trennschärfefunktion der Soll-Trennschärfe entspricht, wird die Berechnungsprozedur beendet.
Soll-Trennschärfe und Ist-Trennschärfe
Beim Berechnen des Stichprobenumfangs ermittelt Minitab möglicherweise, dass die Soll-Trennschärfe nicht mit einem ganzzahligen Wert für den Stichprobenumfang erreicht wird. In solchen Fällen zeigt Minitab den Sollwert der Trennschärfe neben der Ist-Trennschärfe an; bei dieser handelt es sich um einen Wert, der einem ganzzahligen Stichprobenumfang entspricht und dem Sollwert am nächsten kommt, jedoch größer als dieser ist.
