Schritt 1: Berechnete Werte untersuchen
Anhand der eingegebenen Werte für die zwei Eigenschaften berechnet Minitab die Differenz, den Stichprobenumfang oder die Trennschärfe des Tests.
- Differenz (oder Verhältnis)
- Wenn Sie den Stichprobenumfang und die Trennschärfe für den Test eingeben, berechnet Minitab die Differenz (oder das Verhältnis), die bzw. das mit dem Test bei den angegebenen Werten für Trennschärfe und Stichprobenumfang erkannt werden kann. Bei größeren Stichprobenumfängen kann die Differenz (oder das Verhältnis) näher an den Äquivalenzgrenzen liegen. Dieser Wert stellt die Differenz (oder das Verhältnis) zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit dar.
- Stichprobenumfang
- Wenn Sie eine Differenz (oder ein Verhältnis) und einen Trennschärfewert für den Test eingeben, berechnet Minitab, wie groß die Stichprobe sein muss. Wenn Sie den Stichprobenumfang vergrößern, nimmt auch die Trennschärfe des Tests zu. Es empfiehlt sich, dass eine ausreichende Anzahl von Beobachtungen in der Stichprobe vorliegen, um eine angemessene Trennschärfe zu erzielen. Der Stichprobenumfang sollte jedoch nicht so groß sein, dass Zeit und Geld bei der Stichprobennahme vergeudet oder irrelevante Differenzen als statistisch signifikant erkannt werden.
Hinweis
Da der Stichprobenumfang als ganze Zahl angegeben wird, kann die tatsächliche Trennschärfe des Tests etwas höher als der von Ihnen angegebene Trennschärfewert ausfallen.
- Trennschärfe
- Wenn Sie einen Stichprobenumfang und eine Differenz (oder ein Verhältnis) eingeben, berechnet Minitab die Trennschärfe des Tests. Ein Trennschärfewert von mindestens 0,9 wird im Allgemeinen als geeignet angesehen. Eine Trennschärfe von 0,9 bedeutet, dass mit dem Test mit einer Wahrscheinlichkeit von 90 % Äquivalenz nachgewiesen wird, sofern die Differenz (oder das Verhältnis) zwischen den Mittelwerten der Grundgesamtheiten tatsächlich innerhalb der Äquivalenzgrenzen liegt. Wenn ein Äquivalenztest eine zu geringe Trennschärfe aufweist, können Sie die Äquivalenz möglicherweise nicht nachweisen, selbst wenn der Test-Mittelwert und der Referenzmittelwert äquivalent sind. In der Regel weist der Test bei einem kleineren Stichprobenumfang oder einer Differenz (bzw. einem Verhältnis), die (bzw. das) näher an einer Äquivalenzgrenze liegt, eine geringere Trennschärfe zum Nachweisen einer Äquivalenz auf.
Hinweis
Die Definitionen und Anleitungen zur Interpretation in diesem Artikel beziehen sich auf einen Standardtest der Äquivalenz, bei dem die Standard-Alternativhypothese (Untergrenze < Testmittelwert - Referenzmittelwert < Obergrenze) verwendet wird.
Methode
| Trennschärfe für Differenz: | Testmittelwert - Referenzmittelwert |
|---|---|
| Nullhypothese: | Differenz ≤ -0,5 oder Differenz ≥ 0,5 |
| Alternativhypothese: | -0,5 < Differenz < 0,5 |
| α-Niveau: | 0,05 |
Ergebnisse
| Differenz | Stichprobenumfang | Trennschärfe |
|---|---|---|
| 0,3 | 15 | 0,955316 |
Wichtigste Ergebnisse: Differenz, Stichprobenumfang, Trennschärfe
Diese Ergebnisse zeigen, dass die Trennschärfe des Tests zum Nachweisen der Äquivalenz bei einem Stichprobenumfang von 15 und einer Differenz von 0,3 ungefähr 0,96 beträgt. Daher weist der Test eine gute Trennschärfe auf. Anhand der Trennschärfekurve können Sie feststellen, ob der Test bei einer größeren Differenz immer noch eine geeignete Trennschärfe (0,9) erreicht.
Schritt 2: Trennschärfekurve untersuchen
Mit der Trennschärfekurve können Sie den geeigneten Stichprobenumfang oder die angemessene Trennschärfe für einen Test ermitteln.
Die Trennschärfekurve stellt jede Kombination von Trennschärfe und Differenz (oder Verhältnis) für jeden Stichprobenumfang dar, wenn das Signifikanzniveau und die Standardabweichung der verbundenen Differenzen konstant gehalten werden. Jedes Symbol auf der Trennschärfekurve stellt einen Wert dar, der auf der Grundlage der eingegebenen Werte berechnet wurde. Wenn Sie beispielsweise einen Wert für den Stichprobenumfang und einen Wert für die Trennschärfe eingeben, berechnet Minitab die entsprechende Differenz (bzw. das Verhältnis) und zeigt den berechneten Wert in der Grafik an.
Untersuchen Sie die Werte auf der Kurve, um die Differenz (oder das Verhältnis) zwischen Testmittelwert und Referenzmittelwert zu bestimmen, die bei einer bestimmten Trennschärfe und einem bestimmten Stichprobenumfang erkannt werden kann. Ein Trennschärfewert von 0,9 wird im Allgemeinen als geeignet angesehen. Einige Fachleute hingegen erachten einen Trennschärfewert von 0,8 als geeignet. Wenn ein Äquivalenztest eine zu geringe Trennschärfe aufweist, können Sie die Äquivalenz möglicherweise nicht nachweisen, selbst wenn die Mittelwerte der Grundgesamtheiten äquivalent sind. Wenn Sie den Stichprobenumfang vergrößern, nimmt auch die Trennschärfe des Tests zu. Es empfiehlt sich, dass eine ausreichende Anzahl von Beobachtungen in der Stichprobe vorliegen, um eine angemessene Trennschärfe zu erzielen. Der Stichprobenumfang sollte jedoch nicht so groß sein, dass Zeit und Geld bei der Stichprobennahme vergeudet oder irrelevante Differenzen als statistisch signifikant erkannt werden. Im Allgemeinen wird für Differenzen (oder Verhältnisse), die näher an den Äquivalenzgrenzen liegen, eine größere Trennschärfe benötigt, um die Äquivalenz nachzuweisen.
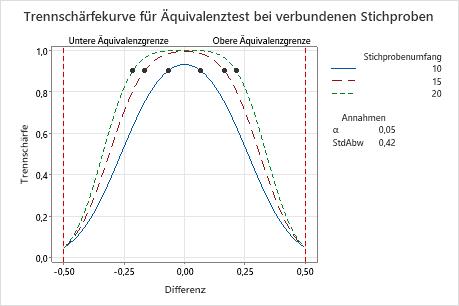
In dieser Grafik veranschaulicht die Trennschärfekurve für einen Stichprobenumfang von 10, dass der Test für eine Differenz von ca. ±0,1 eine Trennschärfe von 0,9 aufweist. Die Trennschärfekurve für einen Stichprobenumfang von 20 zeigt, dass der Test für eine Differenz von ca. ±0,2 eine Trennschärfe von 0,9 aufweist. Bei jeder Kurve nimmt die Trennschärfe des Tests in dem Maße ab und nähert sich α (Alpha ist das Risiko, dass Äquivalenz behauptet wird, während tatsächlich keine vorliegt), in dem sich die Differenz der unteren bzw. oberen Äquivalenzgrenze nähert.
