Methoden und Formeln für Trennschärfe und Stichprobenumfang für Äquivalenztest, 2x2-Crossover-Versuchsplan

In diesem Artikel wird beschrieben, wie die Trennschärfe berechnet wird, wenn Testmittelwert – Referenzmittelwert (Differenz) in Hypothese zu ausgewählt wurde.

Trennschärfe

Sei t_α,v der obere kritische α-Wert (einseitig) für eine t-Verteilung mit v Freiheitsgraden. Die Trennschärfe für die beidseitige Alternativhypothese von Untergrenze < Testmittelwert - Referenzmittelwert < Obergrenze wird wie folgt ausgedrückt:

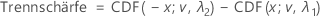
Für die Alternativhypothese von Testmittelwert > Referenzmittelwert oder Testmittelwert – Referenzmittelwert > Untergrenze wird die Trennschärfe wie folgt ausgedrückt:

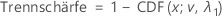
Für die Alternativhypothese von Testmittelwert < Referenzmittelwert oder Testmittelwert – Referenzmittelwert < Obergrenze wird die Trennschärfe wie folgt ausgedrückt:

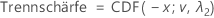
Hierbei ist CDF(x; v, λ) die kumulative Verteilungsfunktion, ausgewertet bei x, für eine nichtzentrale t-Verteilung mit Nichtzentralitätsparameter λ und v Freiheitsgraden.

Freiheitsgrade

Die Freiheitsgrade v werden mit folgender Formel angegeben:

Für Trennschärfeberechnungen wird angenommen, dass n für beide Sequenzen gleich ist.

Nichtzentralitätsparameter

Der Nichtzentralitätsparameter, der der unteren Äquivalenzgrenze entspricht, wird als λ₁ angegeben und wie folgt ausgedrückt:

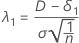
wobei σ die Standardabweichung innerhalb von Probanden darstellt.

Für die Alternativhypothese von Testmittelwert > Referenzmittelwert ist δ₁ = 0.

Der Nichtzentralitätsparameter, der der oberen Äquivalenzgrenze entspricht, wird als λ₂ angegeben und mit der folgenden Formel ausgedrückt:

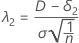
wobei δ₂ die obere Äquivalenzgrenze angibt.

Für die Alternativhypothese von Testmittelwert < Referenzmittelwert ist δ₂ = 0.

Notation

Begriff	Beschreibung
α	Signifikanzniveau für den Test
D	Mittelwert der Testgrundgesamtheit minus Mittelwert der Referenzgrundgesamtheit
δ1	untere Äquivalenzgrenze
δ2	obere Äquivalenzgrenze
n	Anzahl der Teilnehmer in jeder Sequenz. (Für Trennschärfeberechnungen wird angenommen, dass n für beide Sequenzen gleich ist.)

In diesem Artikel wird beschrieben, wie die Trennschärfe berechnet wird, wenn Testmittelwert / Referenzmittelwert (Verhältnis, durch Log-Transformation) in Hypothese zu ausgewählt wurde.

Trennschärfe

Sei t_α,v der obere kritische α-Wert (einseitig) für eine t-Verteilung mit v Freiheitsgraden. Die Trennschärfe für die beidseitige Alternativhypothese von Untergrenze < Testmittelwert / Referenzmittelwert < Obergrenze wird wie folgt ausgedrückt:

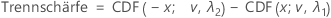
Für die Alternativhypothese von Testmittelwert / Referenzmittelwert > Untergrenze wird die Trennschärfe wie folgt ausgedrückt:

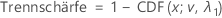
Für die Alternativhypothese von Testmittelwert / Referenzmittelwert < Obergrenze wird die Trennschärfe wie folgt ausgedrückt:

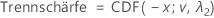
Hierbei ist CDF(x; v, λ) die kumulative Verteilungsfunktion, ausgewertet bei x, für eine nichtzentrale t-Verteilung mit Nichtzentralitätsparameter λ und v Freiheitsgraden.

Freiheitsgrade

Die Freiheitsgrade v werden mit folgender Formel angegeben:

Für Trennschärfeberechnungen wird angenommen, dass n für beide Sequenzen gleich ist.

Nichtzentralitätsparameter

Der Nichtzentralitätsparameter, der der unteren Äquivalenzgrenze entspricht, wird als λ₁ angegeben und wie folgt ausgedrückt:

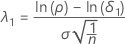
wobei σ die Standardabweichung innerhalb von Probanden darstellt, wie unten beschrieben.

Der Nichtzentralitätsparameter, der der oberen Äquivalenzgrenze entspricht, wird als λ₂ angegeben und wie folgt ausgedrückt:

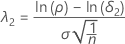
Sigma

Die Standardabweichung σ wird mit dem Variationskoeffizienten (VK) innerhalb von Probanden wie folgt berechnet:

Notation

Begriff	Beschreibung
α	Signifikanzniveau für den Test
ρ	Verhältnis zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit
δ1	untere Äquivalenzgrenze
δ2	obere Äquivalenzgrenze
n	Anzahl der Teilnehmer in jeder Sequenz. (Für Trennschärfeberechnungen wird angenommen, dass n für beide Sequenzen gleich ist.)

Wenn Sie Werte für die Trennschärfe und die Differenz (oder das Verhältnis) angeben, berechnet Minitab den Stichprobenumfang. Minitab bestimmt anhand der geeigneten Trennschärfeformel und eines iterativen Algorithmus den kleinsten Stichprobenumfang n, für den die Trennschärfe größer oder gleich dem angegebenen Wert ist. Die tatsächliche Trennschärfe für n ist wahrscheinlich größer als die angegebene Trennschärfe. Dies ist darauf zurückzuführen, dass n ein diskreter ganzzahliger Wert sein muss und dass wahrscheinlich kein Wert von n genau den angegebenen Trennschärfewert liefert.

Wenn Sie Werte für die Trennschärfe und den Stichprobenumfang angeben, berechnet Minitab Werte für die Differenz. Minitab bestimmt anhand der geeigneten Trennschärfeformel und eines iterativen Algorithmus die größte und/oder kleinste Differenz, für die die Trennschärfe größer oder gleich dem angegebenen Wert ist.

Wenn Sie Werte für die Trennschärfe und den Stichprobenumfang angeben, berechnet Minitab Werte für das Verhältnis. Minitab bestimmt anhand der geeigneten Trennschärfeformel und eines iterativen Algorithmus das größte und/oder kleinste Verhältnis, für das die Trennschärfe größer oder gleich dem angegebenen Wert ist.