In diesem Thema
Trennschärfe für Differenz
In der ersten Zeile der Ausgabe wird angegeben, wie die Hypothesen für den Äquivalenztest ausgedrückt wurden.
„Trennschärfe für Differenz“ gibt an, dass die Hypothesen als Differenz zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit (Testmittelwert – Referenzmittelwert) ausgedrückt wurden.
Trennschärfe für Verhältnis
In der ersten Zeile der Ausgabe wird angegeben, wie die Hypothesen für den Äquivalenztest ausgedrückt wurden.
„Trennschärfe für Verhältnis“ gibt an, dass die Hypothesen als Verhältnis zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit durch Log-Transformation (Testmittelwert / Referenzmittelwert) ausgedrückt wurden.
Nullhypothese und Alternativhypothese
- Nullhypothese
- Minitab testet je nach ausgewählter Alternativhypothese eine oder beide der folgenden Nullhypothesen:
- Die Differenz (oder das Verhältnis) zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit ist größer als die oder gleich der oberen Äquivalenzgrenze.
- Die Differenz (oder das Verhältnis) zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit ist kleiner als die oder gleich der unteren Äquivalenzgrenze.
- Alternativhypothese
- Mit der Alternativhypothese werden eine bzw. beide der folgenden Aussagen getroffen:
- Die Differenz (oder das Verhältnis) zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit ist kleiner als die obere Äquivalenzgrenze.
- Die Differenz (oder das Verhältnis) zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit ist größer als die untere Äquivalenzgrenze.
Interpretation
Verwenden Sie die Nullhypothese und die Alternativhypothese, um die Richtigkeit der Äquivalenzkriterien zu bestätigen und um zu prüfen, ob Sie die geeignete zu testende Alternativhypothese ausgewählt haben.
Methode
| Trennschärfe für Differenz: | Testmittelwert - Referenzmittelwert |
|---|---|
| Nullhypothese: | Differenz ≤ -0,425 oder Differenz ≥ 0,425 |
| Alternativhypothese: | -0,425 < Differenz < 0,425 |
| α-Niveau: | 0,05 |
In diesen Ergebnissen testet Minitab zwei Nullhypothesen:
- Die Differenz zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit ist kleiner oder gleich der unteren Äquivalenzgrenze von −0,425.
- Die Differenz zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit ist größer oder gleich der oberen Äquivalenzgrenze von 0,425.
α (Alpha)
Das Signifikanzniveau (als Alpha oder α bezeichnet) ist das maximal akzeptable Risiko, dass die Nullhypothese zurückgewiesen wird, wenn sie tatsächlich wahr ist (Fehler 1. Art). Wenn Sie beispielsweise einen Äquivalenztest mit den Standardhypothesen durchführen, gibt ein α von 0,05 ein Risiko von 5 % an, dass auf eine Äquivalenz geschlossen wird, wenn die Differenz zwischen dem Testmittelwert und dem Referenzmittelwert tatsächlich nicht innerhalb der Äquivalenzgrenzen liegt.
Das α-Niveau für einen Äquivalenztest bestimmt auch das Konfidenzniveau für das Konfidenzintervall. In der Standardeinstellung beträgt das Konfidenzniveau (1 – α) x 100 %. Wenn Sie die alternative Berechnungsmethode für das Konfidenzintervall anwenden, ist das Konfidenzniveau (1 – 2α) x 100 %.
Interpretation
Verwenden Sie das Signifikanzniveau, um den Trennschärfewert des Tests zu minimieren, wenn die Nullhypothese (H0) wahr ist. Bei höheren Signifikanzniveaus ist der Test trennschärfer, gleichzeitig steigt jedoch die Wahrscheinlichkeit, dass ein Fehler 1. Art auftritt, beim dem die Nullhypothese zurückgewiesen wird, wenn diese tatsächlich wahr ist.
Angenommene Standardabweichung innerhalb von Probanden
Die Standardabweichung innerhalb von Probanden ist die Standardabweichung mehrerer Werte der Antwortvariablen desselben Teilnehmers. Bei diesem Maß der Standardabweichung wird die Größe des Zufallsfehlers in den Messwerten der Antwortvariablen für denselben Teilnehmer geschätzt, nachdem Behandlungseffekte, Periodeneffekte und andere systematische Effekte eliminiert wurden. Größere Werte geben eine stärkere Streuung der Werte der Antwortvariablen für die einzelnen Teilnehmer an.
Interpretation
Wenn Sie eine Analyse der Trennschärfe für einen Äquivalenztest in Bezug auf die Differenz durchführen, müssen Sie die Standardabweichung innerhalb von Probanden eingeben. Diese angenommene Standardabweichung innerhalb von Probanden ist ein Schätzwert der Standardabweichung der Grundgesamtheit.
Minitab verwendet die angenommene Standardabweichung innerhalb von Probanden, um die Trennschärfe des Tests zu berechnen. Höhere Werte der Standardabweichung innerhalb von Probanden verweisen auf eine stärkere Streuung bzw. ein stärkeres „Rauschen“ der Daten, was die statistische Trennschärfe eines Tests reduziert.
Angenommener Variationskoeffizient innerhalb von Probanden
Der Variationskoeffizient innerhalb von Probanden ist der Variationskoeffizient mehrerer Werte der Antwortvariablen desselben Teilnehmers. Der Variationskoeffizient ist gleich der Standardabweichung dividiert durch den Mittelwert.
Bei diesem Maß der Streuung wird die Größe des Zufallsfehlers in den Messwerten der Antwortvariablen für denselben Teilnehmer geschätzt, nachdem Behandlungseffekte, Periodeneffekte und andere systematische Effekte eliminiert wurden. Größere Werte geben eine stärkere Streuung der Werte der Antwortvariablen für die einzelnen Teilnehmer an.
Interpretation
Wenn Sie eine Analyse der Trennschärfe für einen Äquivalenztest in Bezug auf das Verhältnis durchführen, müssen Sie den Variationskoeffizienten innerhalb von Probanden eingeben. Dieser angenommene Variationskoeffizient innerhalb von Probanden ist ein Schätzwert des Variationskoeffizienten der Grundgesamtheit.
Minitab verwendet den angenommenen Variationskoeffizienten innerhalb von Probanden, um die Trennschärfe des Tests zu berechnen. Höhere Werte des Variationskoeffizienten innerhalb von Probanden verweisen auf eine stärkere Streuung bzw. ein stärkeres „Rauschen“ der Daten, was die statistische Trennschärfe eines Tests reduziert.
Differenz
Dieser Wert stellt die Differenz zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit dar.
Hinweis
Die Definitionen und Anleitungen zur Interpretation in diesem Artikel beziehen sich auf einen Standardtest der Äquivalenz, bei dem die Standard-Alternativhypothese (Untergrenze < Testmittelwert - Referenzmittelwert < Obergrenze) verwendet wird.
Interpretation
Wenn Sie den Stichprobenumfang und die Trennschärfe für den Test eingeben, berechnet Minitab die Differenz, die mit dem Test bei den angegebenen Werten für Trennschärfe und Stichprobenumfang erkannt werden kann. Bei größeren Stichprobenumfängen kann die Differenz näher an den Äquivalenzgrenzen liegen.
Wenn Sie die Beziehung zwischen dem Stichprobenumfang und der Differenz bei einer bestimmten Trennschärfe eingehender untersuchen möchten, verwenden Sie die Trennschärfekurve.
Methode
| Trennschärfe für Differenz: | Testmittelwert - Referenzmittelwert |
|---|---|
| Nullhypothese: | Differenz ≤ -0,425 oder Differenz ≥ 0,425 |
| Alternativhypothese: | -0,425 < Differenz < 0,425 |
| α-Niveau: | 0,05 |
Ergebnisse
| Stichprobenumfang | Trennschärfe | Differenz |
|---|---|---|
| 4 | 0,9 | -0,278474 |
| 4 | 0,9 | 0,278474 |
| 8 | 0,9 | -0,329164 |
| 8 | 0,9 | 0,329164 |
| 12 | 0,9 | -0,348248 |
| 12 | 0,9 | 0,348248 |
Diese Ergebnisse zeigen, dass mit zunehmendem Stichprobenumfang die Größe der Differenz zunimmt, die vom Test bei einer bestimmten Trennschärfe erkannt werden kann:
- Bei vier Teilnehmern in jeder Sequenz beträgt die Trennschärfe des Tests mindestens 0,9, wenn die Differenz zwischen ungefähr −0,278 und 0,278 liegt.
- Bei acht Teilnehmern in jeder Sequenz beträgt die Trennschärfe des Tests mindestens 0,9, wenn die Differenz zwischen ungefähr −0,329 und 0,329 liegt.
- Bei zwölf Teilnehmern in jeder Sequenz beträgt die Trennschärfe des Tests mindestens 0,9, wenn die Differenz zwischen ungefähr −0,348 und 0,348 liegt.
Verhältnis
Dieser Wert stellt das Verhältnis zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit dar. Zum Durchführen von Trennschärfeberechnungen für ein Verhältnis müssen Sie eine Hypothese zu Testmittelwert / Referenzmittelwert (Verhältnis, durch Log-Transformation) auswählen.
Hinweis
Die Definitionen und Anleitungen zur Interpretation in diesem Artikel beziehen sich auf einen Äquivalenztest, bei dem die Standard-Alternativhypothese für das Verhältnis (Untergrenze < Testmittelwert / Referenzmittelwert < Obergrenze) verwendet wird.
Interpretation
Wenn Sie den Stichprobenumfang und die Trennschärfe für den Test eingeben, berechnet Minitab das minimale und das maximale Verhältnis, das mit dem Test bei den angegebenen Werten für Trennschärfe und Stichprobenumfang erkannt werden kann. Bei größeren Stichprobenumfängen kann das Verhältnis näher an den Äquivalenzgrenzen liegen.
Wenn Sie die Beziehung zwischen dem Stichprobenumfang und den Verhältnissen bei einer bestimmten Trennschärfe eingehender untersuchen möchten, verwenden Sie die Trennschärfekurve.
Methode
| Trennschärfe für Verhältnis: | Testmittelwert / Referenzmittelwert |
|---|---|
| Nullhypothese: | Verhältnis ≤ 0,9 oder Verhältnis ≥ 1,1 |
| Alternativhypothese: | 0,9 < Verhältnis < 1,1 |
| α-Niveau: | 0,05 |
Ergebnisse
| Stichprobenumfang | Trennschärfe | Verhältnis |
|---|---|---|
| 10 | 0,9 | 0,91749 |
| 10 | 0,9 | 1,07903 |
| 20 | 0,9 | 0,91207 |
| 20 | 0,9 | 1,08544 |
Diese Ergebnisse zeigen, dass mit zunehmendem Stichprobenumfang der Bereich der Verhältnisse zunimmt, die bei einer bestimmten Trennschärfe erkannt werden können:
- Bei 10 Beobachtungen in jeder Sequenz beträgt die Trennschärfe des Tests mindestens 0,9, wenn das Verhältnis zwischen ungefähr 0,92 und 1,08 liegt.
- Bei 20 Beobachtungen in jeder Sequenz beträgt die Trennschärfe des Tests mindestens 0,9 wenn das Verhältnis zwischen ungefähr 0,91 und 1,09 liegt.
Stichprobenumfang
Der Stichprobenumfang gibt die Gesamtzahl der Beobachtungen in der Stichprobe an. Für eine 2x2-Crossover-Untersuchung bezieht sich der Stichprobenumfang auf die Anzahl der Teilnehmer in jeder Sequenz der Untersuchung.
Interpretation
Anhand des Stichprobenumfangs können Sie schätzen, wie viele Beobachtungen Sie benötigen, um bei einer angegebenen Differenz eine bestimmte Trennschärfe für den Äquivalenztest zu erreichen.
Wenn Sie eine Differenz (oder ein Verhältnis) und einen Trennschärfewert für den Test eingeben, berechnet Minitab, wie groß die Stichprobe sein muss. Da der Stichprobenumfang als ganze Zahl angegeben wird, kann die tatsächliche Trennschärfe des Tests etwas höher als der von Ihnen angegebene Trennschärfewert ausfallen.
Wenn Sie den Stichprobenumfang vergrößern, nimmt auch die Trennschärfe des Tests zu. Es empfiehlt sich, dass eine ausreichende Anzahl von Beobachtungen in der Stichprobe vorliegen, um eine angemessene Trennschärfe zu erzielen. Der Stichprobenumfang sollte jedoch nicht so groß sein, dass Zeit und Geld bei der Stichprobennahme vergeudet oder irrelevante Differenzen als statistisch signifikant erkannt werden.
Wenn Sie die Beziehung zwischen dem Stichprobenumfang und der Differenz (oder dem Verhältnis), die bzw. das mit dem Test bei einer bestimmten Trennschärfe erkannt werden kann, eingehender untersuchen möchten, verwenden Sie die Trennschärfekurve.
Methode
| Trennschärfe für Differenz: | Testmittelwert - Referenzmittelwert |
|---|---|
| Nullhypothese: | Differenz ≤ -0,425 oder Differenz ≥ 0,425 |
| Alternativhypothese: | -0,425 < Differenz < 0,425 |
| α-Niveau: | 0,05 |
Ergebnisse
| Differenz | Stichprobenumfang | Soll-Trennschärfe | Ist-Trennschärfe |
|---|---|---|---|
| 0,0 | 2 | 0,9 | 0,978589 |
| 0,1 | 2 | 0,9 | 0,931544 |
| 0,2 | 3 | 0,9 | 0,972795 |
| 0,3 | 6 | 0,9 | 0,943646 |
| 0,4 | 107 | 0,9 | 0,900500 |
Diese Ergebnisse zeigen, dass Sie einen größeren Stichprobenumfang benötigen, um eine bestimmte Trennschärfe zu erreichen, wenn die Differenz zunimmt und sich an die Äquivalenzgrenze annähert. Bei einer Differenz von 0,1 benötigen Sie lediglich zwei Teilnehmer pro Sequenz, um eine Trennschärfe von 0,9 zu erreichen. Bei einer Differenz von 0,4, benötigen Sie mindestens 107 Teilnehmer in jeder Sequenz, um eine Trennschärfe von 0,9 zu erreichen.
Trennschärfe
Die Trennschärfe eines Äquivalenztests ist die Wahrscheinlichkeit, mit der der Test nachweist, dass die Differenz innerhalb der Äquivalenzgrenzen liegt, wenn dies tatsächlich der Fall ist. Die Trennschärfe eines Äquivalenztests wird vom Stichprobenumfang, der Differenz, den Äquivalenzgrenzen, der Streuung der Daten und dem Signifikanzniveau des Tests beeinflusst.
Weitere Informationen finden Sie unter Trennschärfe für Äquivalenztests.
Interpretation
Wenn Sie einen Stichprobenumfang und eine Differenz (oder ein Verhältnis) eingeben, berechnet Minitab die Trennschärfe des Tests. Ein Trennschärfewert von mindestens 0,9 wird im Allgemeinen als geeignet angesehen. Eine Trennschärfe von 0,9 bedeutet, dass mit dem Test mit einer Wahrscheinlichkeit von 90 % Äquivalenz nachgewiesen wird, sofern die Differenz (oder das Verhältnis) zwischen den Mittelwerten der Grundgesamtheiten tatsächlich innerhalb der Äquivalenzgrenzen liegt. Wenn ein Äquivalenztest eine zu geringe Trennschärfe aufweist, können Sie die Äquivalenz möglicherweise nicht nachweisen, selbst wenn der Test-Mittelwert und der Referenzmittelwert äquivalent sind.
In der Regel weist der Test bei einem kleineren Stichprobenumfang oder einer Differenz (bzw. einem Verhältnis), die (bzw. das) näher an einer Äquivalenzgrenze liegt, eine geringere Trennschärfe zum Nachweisen einer Äquivalenz auf.
Methode
| Trennschärfe für Differenz: | Testmittelwert - Referenzmittelwert |
|---|---|
| Nullhypothese: | Differenz ≤ -0,425 oder Differenz ≥ 0,425 |
| Alternativhypothese: | -0,425 < Differenz < 0,425 |
| α-Niveau: | 0,05 |
Ergebnisse
| Differenz | Stichprobenumfang | Trennschärfe |
|---|---|---|
| 0,3 | 8 | 0,984946 |
| 0,3 | 12 | 0,999089 |
| 0,4 | 8 | 0,189487 |
| 0,4 | 12 | 0,244815 |
In diesen Ergebnissen beträgt die Trennschärfe für eine Differenz von 0,3 ungefähr 0,98 bei einem Stichprobenumfang von 8 und 0,99 bei einem Stichprobenumfang von 15. Für eine Differenz von 0,4 beträgt die Trennschärfe ungefähr 0,19 bei einem Stichprobenumfang von 8 und 0,24 bei einem Stichprobenumfang von 12.
Trennschärfekurve
Die Trennschärfekurve zeigt die Trennschärfe des Tests im Vergleich zur Differenz zwischen dem Testmittelwert und dem Referenzmittelwert.
Interpretation
Mit der Trennschärfekurve können Sie den geeigneten Stichprobenumfang oder die angemessene Trennschärfe für einen Test ermitteln.
Die Trennschärfekurve stellt jede Kombination von Trennschärfe und Differenz (oder Verhältnis) für jeden Stichprobenumfang dar, wenn das Signifikanzniveau und die Standardabweichung (oder der Variationskoeffizient) konstant gehalten werden. Jedes Symbol auf der Trennschärfekurve stellt einen Wert dar, der auf der Grundlage der eingegebenen Werte berechnet wurde. Wenn Sie beispielsweise einen Wert für den Stichprobenumfang und einen Wert für die Trennschärfe eingeben, berechnet Minitab die entsprechende Differenz (bzw. das Verhältnis) und zeigt den berechneten Wert in der Grafik an.
Untersuchen Sie die Werte auf der Kurve, um die Differenz (oder das Verhältnis) zwischen Testmittelwert und Referenzmittelwert zu bestimmen, die bei einer bestimmten Trennschärfe und einem bestimmten Stichprobenumfang erkannt werden kann. Ein Trennschärfewert von 0,9 wird im Allgemeinen als geeignet angesehen. Einige Fachleute hingegen erachten einen Trennschärfewert von 0,8 als geeignet. Wenn ein Äquivalenztest eine zu geringe Trennschärfe aufweist, können Sie die Äquivalenz möglicherweise nicht nachweisen, selbst wenn die Mittelwerte der Grundgesamtheiten äquivalent sind. Wenn Sie den Stichprobenumfang vergrößern, nimmt auch die Trennschärfe des Tests zu. Es empfiehlt sich, dass eine ausreichende Anzahl von Beobachtungen in der Stichprobe vorliegen, um eine angemessene Trennschärfe zu erzielen. Der Stichprobenumfang sollte jedoch nicht so groß sein, dass Zeit und Geld bei der Stichprobennahme vergeudet oder irrelevante Differenzen als statistisch signifikant erkannt werden. Im Allgemeinen wird für Differenzen (oder Verhältnisse), die näher an den Äquivalenzgrenzen liegen, eine größere Trennschärfe benötigt, um die Äquivalenz nachzuweisen.
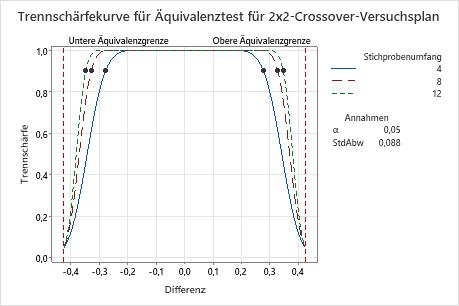
In dieser Grafik zeigen die Trennschärfekurven für alle Stichprobenumfänge, dass der Test eine ausreichende Trennschärfe (≥ 0,9) für eine Differenz von bis zu ca. ±0,25 aufweist. Die Stichprobenumfänge geben die Anzahl der Teilnehmer in jeder Sequenz an. Die Trennschärfekurve für einen Stichprobenumfang von 4 zeigt, dass der Test für eine Differenz von ca. ±0,28 eine Trennschärfe von 0,9 aufweist. Die Trennschärfekurve für einen Stichprobenumfang von 12 zeigt, dass der Test für eine Differenz von ca. ±0,33 eine Trennschärfe von 0,9 aufweist. Beachten Sie, dass sich die bei einer Trennschärfe von 0,9 erkennbare Differenz durch Steigern des Stichprobenumfangs auf 12 nur geringfügig erhöht. Bei jeder Kurve nimmt die Trennschärfe des Tests in dem Maße ab und nähert sich α (Alpha ist das Risiko, dass Äquivalenz behauptet wird, während tatsächlich keine vorliegt), in dem sich die Differenz der unteren bzw. oberen Äquivalenzgrenze nähert.
