Ein Verpackungstechniker möchte ein neues Verfahren zum Versiegeln von Snackbeuteln testen. Die beim Öffnen der Beutel aufzuwendende Kraft muss innerhalb von 10 % des Sollwerts von 4,2 N (Newton) liegen. Ehe der Techniker die Daten für einen Äquivalenztest bei einer Stichprobe erfasst, bestimmt er anhand einer Berechnung von Trennschärfe und Stichprobenumfang, wie groß die Stichprobe sein muss, um eine Trennschärfe von 80 % (0,8) zu erzielen. Auf der Grundlage früherer Stichproben schätzt er die Standardabweichung der Grundgesamtheit auf 0,332.
- Wählen Sie aus.
- Wählen Sie unter Was möchten Sie ermitteln? (Alternativhypothese) die Option Untergrenze < Testmittelwert - Sollwert < Obergrenze aus.
- Geben Sie im Feld Untergrenze den Wert –0,42 ein. Geben Sie im Feld Obergrenze den Wert 0,42 ein.
- Geben Sie im Feld Differenzen (innerhalb der Grenzen) die Werte 0 0,1 0,2 0,3 ein.
- Geben Sie im Feld Trennschärfewerte den Wert 0,8 ein.
- Geben Sie im Feld Standardabweichung den Wert 0,332 ein.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
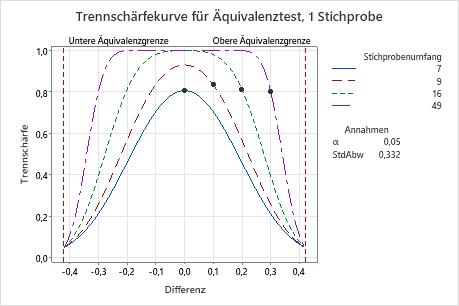
Wenn die Differenz 0 beträgt (die mittlere Kraft entspricht dem Sollwert), benötigt der Techniker einen Stichprobenumfang von 7, um eine Trennschärfe von 0,8 zu erreichen. Verwendet er einen Stichprobenumfang von 9, beträgt die Trennschärfe des Tests für eine Differenz von 0 mehr als 0,9.
Wenn die Differenz näher an der oberen Äquivalenzgrenze (0,42) liegt, benötigt der Techniker einen größeren Stichprobenumfang, um die gleiche Trennschärfe zu erreichen. Für eine Differenz von 0,3 wird z. B. ein Stichprobenumfang von 49 benötigt, um eine Trennschärfe von 0,8 zu erreichen.
Bei jedem Stichprobenumfang nimmt die Trennschärfe des Tests in dem Maße ab und nähert sich α (Alpha ist das Risiko, dass Äquivalenz behauptet wird, während tatsächlich keine vorliegt), in dem sich die Differenz der unteren bzw. oberen Äquivalenzgrenze nähert.
Methode
| Trennschärfe für Differenz: | Testmittelwert - Sollwert |
|---|---|
| Nullhypothese: | Differenz ≤ -0,42 oder Differenz ≥ 0,42 |
| Alternativhypothese: | -0,42 < Differenz < 0,42 |
| α-Niveau: | 0,05 |
| Angenommene Standardabweichung: | 0,332 |
Ergebnisse
| Differenz | Stichprobenumfang | Soll-Trennschärfe | Ist-Trennschärfe |
|---|---|---|---|
| 0,0 | 7 | 0,8 | 0,805075 |
| 0,1 | 9 | 0,8 | 0,834590 |
| 0,2 | 16 | 0,8 | 0,811465 |
| 0,3 | 49 | 0,8 | 0,802154 |