Interpretieren aller Statistiken für Sequenzentest

Hier finden Sie Definitionen und Anleitungen zur Interpretation für alle Statistiken, die für einen Sequenzentest bereitgestellt werden.

In diesem Thema

N
K
≤ K und > K
Nullhypothese und Alternativhypothese
Beobachtete Sequenzzahl und erwartete Sequenzzahl
p-Wert

N

Der Stichprobenumfang (N) gibt die Gesamtzahl der Beobachtungen in der Stichprobe an. Der Stichprobenumfang wirkt sich auf die erwartete Anzahl von Sequenzen und den p-Wert aus.

K

K ist der Wert des Vergleichskriteriums. In der Standardeinstellung ist K der Mittelwert der Stichprobendaten. Sie können jedoch auch einen anderen Wert angeben, z. B. den Median. Minitab verwendet K, um die beobachtete Sequenzzahl zu berechnen.

≤ K und > K

Die Anzahl der Beobachtungen größer als K ist die Anzahl der Beobachtungen, die größer als der Wert des Vergleichskriteriums sind, bei dem es sich standardmäßig um den Mittelwert handelt. Die Anzahl der Beobachtungen kleiner als K ist die Anzahl der Beobachtungen, die kleiner oder gleich dem Vergleichskriterium sind. Minitab verwendet diese Werte, um den p-Wert zu berechnen.

Nullhypothese und Alternativhypothese

Die Nullhypothese und die Alternativhypothese sind zwei einander ausschließende Aussagen über die Reihenfolge der Daten. In einem Hypothesentest werden Stichprobendaten verwendet, um zu bestimmen, ob die Nullhypothese zurückgewiesen werden sollte.

Nullhypothese: Die Reihenfolge der Daten ist zufällig.
Alternativhypothese: Die Reihenfolge der Daten ist nicht zufällig.

Beobachtete Sequenzzahl und erwartete Sequenzzahl

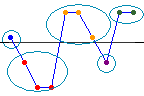
Die beobachtete Sequenzzahl ist die Anzahl der Gruppen von Beobachtungen, die über oder unter dem Vergleichskriterium K liegen. K wird von der Linie dargestellt. Dieses Beispiel enthält fünf Sequenzen.

Die erwartete Sequenzzahl ist der Mittelwert der Verteilung von Sequenzen in einer Stichprobe bei einer zufälligen Datenreihe. Wenn die Anzahl der beobachteten Sequenzen wesentlich größer oder kleiner als die Anzahl der erwarteten Sequenzen ist, weisen die Daten wahrscheinlich keine zufällige Reihenfolge auf. Vergleichen Sie den p-Wert mit dem Signifikanzniveau, um zu bestimmen, ob die Reihenfolge der Daten zufällig ist.

p-Wert

Der p-Wert ist das Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.

Interpretation

Verwenden Sie den p-Wert, um zu bestimmen, ob die Reihenfolge der Daten zufällig ist.

Vergleichen Sie den p-Wert mit dem Signifikanzniveau, um zu bestimmen, ob die Reihenfolge der Daten zufällig ist. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko von 5 %, dass auf eine zufällige Reihenfolge der Daten geschlossen wird, wenn dies tatsächlich nicht der Fall ist.

p-Wert ≤ α: Die Reihenfolge der Daten ist nicht zufällig (H₀ zurückweisen): Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass die Reihenfolge der Daten nicht zufällig ist.
p-Wert > α: Es kann nicht gefolgert werden, dass die Reihenfolge der Daten nicht zufällig ist (H₀ nicht zurückweisen): Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen keine hinreichenden Hinweise für die Schlussfolgerung vor, dass die Reihenfolge der Daten nicht zufällig ist.