Methoden und Formeln für Mann-Whitney-Test

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Teststatistik
Bilden einer Rangfolge gebundener Werte
p-Wert
Punktschätzung
Konfidenzintervall

Teststatistik

Minitab berechnet die Mann-Whitney-Statistik wie folgt:

Minitab bildet eine Rangfolge der zwei kombinierten Stichproben. Minitab weist der kleinsten Beobachtung den Rang 1, der zweitkleinsten Beobachtung den Rang 2 usw. zu.
Wenn mindestens zwei Beobachtungen gebunden sind, weist Minitab jeder dieser Beobachtungen den durchschnittlichen Rang zu.
Minitab summiert die Ränge für die erste Stichprobe.

Bilden einer Rangfolge gebundener Werte

Gebundene Werte treten auf, wenn mindestens zwei Beobachtungen gleich sind. Wenn Ihre Daten gebundene Werte aufweisen, bildet Minitab die Rangfolge der Daten wie folgt:

Die Beobachtungen werden in aufsteigender Reihenfolge sortiert.
Den einzelnen Beobachtungen werden Ränge zugewiesen, als ob keine Bindungen vorliegen würden.
Bei einer Gruppe gebundener Werte wird der Durchschnitt der entsprechenden Ränge ermittelt, und jedem gebundenen Wert in dieser Gruppe wird dieser Wert als neuer Rang zugewiesen.

Beispiel

Eine Stichprobe enthält 9 Beobachtungen: 2,4; 5,3; 2,4; 4,0; 1,2; 3,6; 4,0; 4,3 und 4,0.

	Beobachtung	Rang (unter der Annahme, dass keine Bindungen vorliegen)	Rang
	1,2	1	1
Gebunden	2,4	2	2,5
Gebunden	2,4	3	2,5
	3,6	4	4
Gebunden	4,0	5	6
	4,0	6	6
	4,0	7	6
	4,3	8	8
	5,3	9	9

Minitab verwendet zudem die folgenden Informationen, um die Teststatistik zu berechnen:

Die Anzahl der Gruppen von Bindungen beträgt 2.
Die Anzahl gebundener Werte in der ersten Gruppe beträgt 2.
Die Anzahl gebundener Werte in der zweiten Gruppe beträgt 3.

p-Wert

Formel

Beim Mann-Whitney-Test wird eine Normal-Approximation verwendet, um den p-Wert des Tests zu bestimmen.

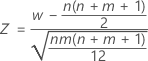folgt annähernd einer Normalverteilung mit dem Mittelwert 0 und der Standardabweichung 1, N(0;1).

Für den p-Wert der Normal-Approximation für die drei Alternativhypothesen wird eine Kontinuitätskorrektur von 0,5 angewendet.

Alternativhypothese	p-Wert
H₁: η₁ > η₂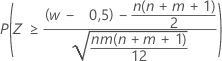
H₁: η₁ < η₂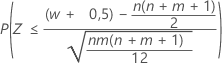
H₁: η₁ ≠ η₂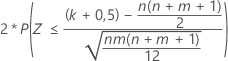

Wenn die Daten Bindungen enthalten, korrigiert Minitab den p-Wert, indem der Nenner der oben genannten Z-Statistik durch Folgendes ersetzt wird:

Der korrigierte p-Wert ist normalerweise genauer als der nicht korrigierte p-Wert. Der nicht korrigierte p-Wert ist jedoch der konservativere Schätzwert, da er für ein bestimmtes Paar von Stichproben stets größer als der korrigierte p-Wert ist.

Notation

Begriff	Beschreibung
W	Mann-Whitney-Teststatistik
n	Umfang von Stichprobe 1
m	Umfang von Stichprobe 2
η₁	Median von Stichprobe 1
η₂	Median von Stichprobe 2
k
i	1, 2, …, I
I	Anzahl der Gruppen von Bindungen
t_i	Anzahl gebundener Werte in der i-ten Gruppe von Bindungen

Punktschätzung

Der Approximationsalgorithmus, mit dem Minitab die Punktschätzung von η₁ – η₂ berechnet, wird in diesem Artikel beschrieben: J. W. McKean und T.A. Ryan, Jr. (1977). „An Algorithm for Obtaining Confidence Intervals and Point Estimates Based on Ranks in the Two Sample Location Problem“, Transactions on Mathematical Software, S. 183–185.

Konfidenzintervall

Das Konfidenzintervall von η₁ – η₂ wird definiert als der Bereich der Werte von η₁ – η₂, für die die Nullhypothese nicht zurückgewiesen wird.

Die Methode, mit der Minitab das Konfidenzintervall berechnet, wird in diesem Artikel beschrieben: J. W. McKean und T. A. Ryan, Jr. (1977). „An Algorithm for Obtaining Confidence Intervals and Point Estimates Based on Ranks in the Two Sample Location Problem“, Transactions on Mathematical Software, S. 183-185.