In diesem Thema
S
Die Teststatistik weist annähernd eine Chi-Quadrat-Verteilung (χ2) mit (k – 1) Freiheitsgraden auf. Wenn die Daten innerhalb eines oder mehrerer Blöcke Bindungen aufweisen, verwendet Minitab den durchschnittlichen Rang und gibt eine Teststatistik aus, die für Bindungen korrigiert wurde. Einzelheiten zu dieser Methode können Sie M. Hollander und D. A. Wolfe (1973)1 entnehmen.
Formel
Zum Berechnen der Chi-Quadrat-Teststatistik bildet Minitab separat innerhalb der einzelnen Blöcke eine Rangfolge der Daten und summiert die Ränge für jede Behandlung.
Wenn die Daten keine Bindungen aufweisen, lautet die Formel wie folgt:
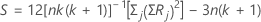
Wenn die Daten Bindungen aufweisen, lautet die Formel wie folgt:

Hierbei ist C ein Korrekturfaktor, der Folgendem entspricht:
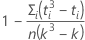
Notation
| Begriff | Beschreibung |
|---|---|
| j | 1, 2, ..., k |
| kk | Anzahl der Behandlungsbedingungen |
| n | Anzahl der Blöcke |
| Rj | Summe der Ränge für Behandlung j |
| ii | 1, 2, ..., m |
| m | Anzahl der Gruppen von Bindungen |
| ti | Anzahl gebundener Werte in der i-ten Gruppe von Bindungen |
- M. Hollander und D. A. Wolfe (1973). Nonparametric Statistical Methods, John Wiley & Sons, Inc.
Gesamtmedian
Betrachten Sie die folgenden Daten, um zu verstehen, wie die Behandlungseffekte, die Blockmediane und der Gesamtmedian berechnet werden.
| Block | ||||
| Behandlung | 1 | 2 | 3 | 4 |
| 1 | 0,15 | 0,26 | 0,23 | 0,99 |
| 2 | 0,55 | 0,26 | −0,22 | 0,99 |
| 3 | 0,55 | 0,66 | 0,77 | 0,99 |
Um die Behandlungseffekte zu berechnen (Doksum-Methode1), ermitteln Sie zunächst die Median-Differenz zwischen Behandlungspaaren. Die paarweisen Differenzen für Behandlung 1 minus Behandlung 2 sind 0,15 – 0,55 = −0,4; 0,26 – 0,26 = 0; 0,23 – (−0,22) = 0,45 und 0,99 – 0,99 = 0. Der Median der Differenzen beträgt 0. Die Berechnung für die anderen beiden Paare liefert −0,4 für Behandlung 1 minus Behandlung 3 und −0,2 für Behandlung 2 minus Behandlung 3.
Der Effekt für die einzelnen Behandlungen ist der Durchschnitt der Median-Differenzen der betreffenden Behandlungen mit allen anderen Behandlungen (einschließlich mit sich selbst). Für die Daten in diesem Beispiel gilt Folgendes: Effekt(2) = [Median (2 – 1) + Median (2 – 2) + Median (2 – 3)]/3 = (0,00 + 0,00 – 0,20)/3 = −0,0667. Ebenso gilt Effekt(1) = −0,1333 und Effekt(3) = 0,20.
Zum Berechnen von korrigierten Blockmedianen korrigieren Sie jede Beobachtung, indem Sie den entsprechenden Behandlungseffekt von der Beobachtung subtrahieren. Korrigierte Blockmediane sind einfach die Mediane dieser korrigierten Daten, die innerhalb der einzelnen Blöcke berechnet werden. Der Gesamtmedian ist der Median der korrigierten Blockmediane. Der geschätzte Median für jede Behandlungsstufe entspricht dem Behandlungseffekt plus dem Gesamtmedian.
- M. Hollander und D. A. Wolfe (1973). Nonparametric Statistical Methods, John Wiley & Sons, Inc., S. 158–161.
Bilden einer Rangfolge gebundener Werte
- Die Beobachtungen werden in aufsteigender Reihenfolge sortiert.
- Den einzelnen Beobachtungen werden Ränge zugewiesen, als ob keine Bindungen vorliegen würden.
- Bei einer Gruppe gebundener Werte wird der Durchschnitt der entsprechenden Ränge ermittelt, und jedem gebundenen Wert in dieser Gruppe wird dieser Wert als neuer Rang zugewiesen.
Beispiel
Eine Stichprobe enthält 9 Beobachtungen: 2,4; 5,3; 2,4; 4,0; 1,2; 3,6; 4,0; 4,3 und 4,0.
| Beobachtung | Rang (unter der Annahme, dass keine Bindungen vorliegen) | Rang |
|---|---|---|
| 1,2 | 1 | 1 |
| 2,4 | 2 | 2,5 |
| 2,4 | 3 | 2,5 |
| 3,6 | 4 | 4 |
| 4,0 | 5 | 6 |
| 4,0 | 6 | 6 |
| 4,0 | 7 | 6 |
| 4,3 | 8 | 8 |
| 5,3 | 9 | 9 |
- Anzahl der Gruppen von Bindungen = 2
- Anzahl gebundener Werte in der ersten Gruppe = 2
- Anzahl gebundener Werte in der zweiten Gruppe = 3
