Methoden und Formeln für Wilcoxon-Test, 1 Stichprobe

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Paarweise Mittelwerte
Geschätzter Median
Wilcoxon-Statistik
p-Wert
Konfidenzintervall

Paarweise Mittelwerte

Paarweise Mittelwerte (die auch als Walsh-Mittelwerte bezeichnet werden) sind die Mittelwerte für jedes mögliche Paar von Werten im Datensatz, einschließlich des Paars aus jedem Wert mit sich selbst.

Formel

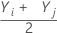= alle paarweisen Mittelwerte für i ≤ j.

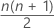= Gesamtzahl der paarweisen Mittelwerte

Notation

Begriff	Beschreibung
Y_i	i-ter Wert im Datensatz
Y_j	j-ter Wert im Datensatz
n	Stichprobenumfang

Geschätzter Median

Seien W_{( 1 )} < W_{( 2 )} < ... < W_{( M )} die geordneten Werte von paarweisen Mittelwerten (auch als Walsh-Mittelwerte bezeichnet), wobei M = n(n+1)/2. Bei ungeradem M ist der geschätzte Median der mittlere Wert. Bei geradem M ist der geschätzte Median der Durchschnitt der beiden mittleren Werte. Minitab berechnet die Punktschätzung des Medians der Grundgesamtheit mit einem Algorithmus nach Johnson und Mizoguchi (1978)¹.

D. B. Johnson und T. Mizoguchi (1978). „Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm“, SIAM Journal of Computing 7, S. 147-153.

Wilcoxon-Statistik

Die Wilcoxon-Statistik entspricht der Anzahl der paarweisen Mittelwerte (auch als Walsh-Mittelwerte bezeichnet), die größer als der Hypothesen-Median sind, plus der halben Anzahl der paarweisen Mittelwerte, die gleich dem Hypothesen-Median sind. Die Wilcoxon-Statistik wird mit W angegeben. Minitab berechnet die Teststatistik mit einem Algorithmus nach Johnson und Mizoguchi (1978)¹.

D. B. Johnson und T. Mizoguchi (1978). „Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm“, SIAM Journal of Computing 7, S. 147-153.

p-Wert

Die Wilcoxon-Teststatistik W ist die Summe der Ränge der Beobachtungen, die den Hypothesen-Median überschreiten. Minitab berechnet die Teststatistik anhand von paarweisen Mittelwerten (Walsh-Mittelwerten), die in Johnson und Mizoguchi¹ beschrieben werden:

Die Anzahl der Beobachtungen N wird für jede Beobachtung, die gleich dem Hypothesen-Median ist, um 1 verringert. Der resultierende Stichprobenumfang ist n.
Die Beobachtungen, die gleich dem Hypothesen-Median sind, werden ausgeschlossen. Es werden n(n + 1) / 2 paarweise Walsh-Mittelwerte (Y_i + Y_j) / 2 für i ≤ j der Beobachtungen berechnet.

Bei großen Stichprobenumfängen entspricht die Verteilung von W annähernd einer Normalverteilung. Insbesondere heißt dies:

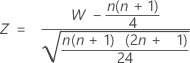folgt annähernd einer Normalverteilung mit dem Mittelwert 0 und der Standardabweichung 1, N(0;1).

Für den p-Wert der Normal-Approximation für die drei Alternativhypothesen wird eine Kontinuitätskorrektur von 0,5 angewendet.

Alternativhypothese	p-Wert
H₁: Median > Hypothesen-Median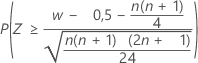
H₁: Median < Hypothesen-Median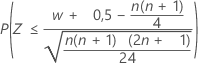
H₁: Median ≠ Hypothesen-Median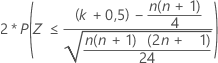

Notation

Begriff	Beschreibung
n	beobachtete Anzahl der Datenpunkte, nachdem die Beobachtungen, die gleich dem Wert des Hypothesen-Medians sind, ausgeschlossen wurden
W	Wilcoxon-Teststatistik
w	Anzahl der Walsh-Mittelwerte, die den Hypothesen-Median überschreiten, plus der halben Anzahl der Walsh-Mittelwerte, die gleich dem Hypothesen-Median sind
k

D. B. Johnson und T. Mizoguchi (1978). „Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm“, SIAM Journal of Computing 7, S. 147-153.

Konfidenzintervall

Das Konfidenzintervall ist die Gruppe von Werten (d), für die der Test von H₀: Median = d nicht zugunsten von H₁: Median ≠ d zurückgewiesen wird, wobei das Konfidenzniveau (α = 1 - (Prozentsatz der Konfidenz) / 100) verwendet wird. Beim Wilcoxon-Test bei einer Stichprobe wird nicht immer das angegebene Konfidenzniveau erreicht, da die Teststatistik des Wilcoxon-Tests diskret ist. Daher verwendet Minitab eine Normal-Approximation mit einer Kontinuitätskorrektur, um das nächste erreichbare Konfidenzniveau zu berechnen.