In diesem Thema
p-Wert für die exakte Methode
Minitab verwendet die Binomialverteilung, um den p-Wert für Stichproben mit einem Umfang von bis zu 50 (n ≤ 50) zu berechnen. Für einen Stichprobenumfang n (nachdem alle Beobachtungen ausgeschlossen wurden, die gleich dem Wert des Hypothesen-Medians sind) und eine Wahrscheinlichkeit des Ereignisses von p = 0,5 gemäß der Nullhypothese, hängt die Berechnung des p-Werts von der Alternativhypothese ab.
| Alternativhypothese | p-Wert |
|---|---|
| H1: Median > Hypothesen-Median |  |
| H1: Median < Hypothesen-Median |  |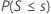
| H1: Median ≠ Hypothesen-Median |  |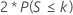
Notation
| Begriff | Beschreibung |
|---|---|
| n | beobachtete Anzahl der Datenpunkte, nachdem die Beobachtungen, die gleich dem Wert des Hypothesen-Medians sind, ausgeschlossen wurden |
| s | beobachtete Anzahl der Datenpunkte, die größer als der Hypothesen-Median sind |
| S | Zufallsvariable, die einer Binomialverteilung mit n Versuchen und einer Ereigniswahrscheinlichkeit von 0,5 folgt, B(n; 0,5) |
| k |  |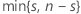
p-Wert für die Methode der Normal-Approximation
Minitab verwendet eine Normal-Approximation der Binomialverteilung, um den p-Wert für Stichproben zu berechnen, die größer als 50 (n > 50) sind. Insbesondere heißt dies:
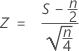folgt annähernd einer Normalverteilung mit dem Mittelwert 0 und der Standardabweichung 1, N(0;1).
wobei S, die Anzahl der Beobachtungen über dem Median, gemäß der Nullhypothese eine Binomialverteilung mit n Versuchen und p = 0,5 als Erfolgswahrscheinlichkeit aufweist, B(n; 0,5).
Für den p-Wert der Normal-Approximation für die drei Alternativhypothesen wird eine Kontinuitätskorrektur von 0,5 angewendet.
| Alternativhypothese | p-Wert |
|---|---|
| H1: Median > Hypothesen-Median |  |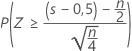
| H1: Median < Hypothesen-Median |  |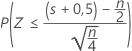
| H1: Median ≠ Hypothesen-Median |  |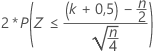
Notation
| Begriff | Beschreibung |
|---|---|
| n | beobachtete Anzahl der Datenpunkte, nachdem die Beobachtungen, die gleich dem Wert des Hypothesen-Medians sind, ausgeschlossen wurden |
| s | beobachtete Anzahl der Datenpunkte, die größer als der Hypothesen-Median sind |
| S | Zufallsvariable, die eine Binomialverteilung mit n Versuchen und p = 0,5 als Erfolgswahrscheinlichkeit aufweist, B(n; 0,5) |
| k |  |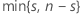
Konfidenzintervall
Verfahren
- Minitab ordnet die Beobachtungen so an, dass X(1) < X(2) < ... < X(n) gilt, wobei X(i) die i-kleinste Beobachtung darstellt.
- Für das angegebene Konfidenzniveau (γ) ist das erste Intervall das nächstgelegene genaue Intervall mit Konfidenz ≤ γ. Das dritte Intervall ist das nächstgelegene genaue Intervall mit Konfidenz ≥ γ. Sei d die größte ganze Zahl, bei der Folgendes gilt:
- P (B < d) < (1 – γ) / 2.
B weist eine Binomialverteilung mit den Parametern Stichprobenumfang n und Wahrscheinlichkeit des Ereignisses p = 0,5 auf.
- Das erste Intervall erstreckt sich von X(d + 1) bis X(n – d), und das dritte Intervall erstreckt sich von X(d ) bis X(n – d + 1).
- Minitab berechnet das mittlere Konfidenzintervall durch ein Verfahren der nichtlinearen Interpolation (NLI), das von Hettmansperger und Sheather1 entwickelt wurde. Seien γd + 1 das Konfidenzniveau des ersten Intervalls und γd das Konfidenzniveau des dritten Intervalls.
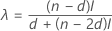
Der untere Endpunkt des Interpolationsintervalls wird durch folgende Formel angegeben:
- X(d) + λ (X(d + 1) – X(d))
Der obere Endpunkt wird durch folgende Formel angegeben:
- X(n – d + 1) – λ (X(n – d + 1) – X(n – d))
