Methoden und Formeln für Testmittelwert - Referenzmittelwert für Äquivalenztest, verbundene Stichproben

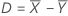
Notation

Begriff	Beschreibung
D	Differenz
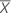	Testmittelwert
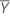	Referenzmittelwert

In Minitab wird der Standardfehler (SE) der Differenz mit der folgenden Formel berechnet:

Hierbei ist S die Standardabweichung der Differenzen, die wie unten definiert ist.

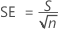
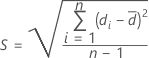
Notation

Begriff	Beschreibung
SE	Standardfehler der Differenz
S	Standardabweichung der Differenzen
n	Anzahl der Beobachtungspaare
di	Paarweise Differenzen (X i - Yi), i = 1, ..., n
	Durchschnitt der paarweisen Differenzen

k₁ sei der Wert, den Sie für die Untergrenze angeben, und k₂ sei der Wert, den Sie für die Obergrenze angeben. Die untere Äquivalenzgrenze δ₁ wird standardmäßig mit der folgenden Formel angegeben:

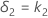
Die obere Äquivalenzgrenze δ₂ wird wie folgt angegeben:

Notation

Begriff	Beschreibung
v	Freiheitsgrade
n	Anzahl der Beobachtungspaare

100(1 – α)%-KI

Standardmäßig wird das 100(1 – α)%-Konfidenzintervall (KI) für die Äquivalenz in Minitab mit der folgenden Formel berechnet:

KI = [min(C, D_u), max(C, D_o)]

Dabei gilt Folgendes:

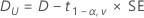
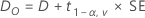
100(1 – 2α)%-KI

Wenn Sie die Option für die Verwendung des 100(1 – 2 α)%-KI auswählen, wird das KI mit der folgenden Formel angegeben:

KI = [D_u, D_o]

Einseitige Intervalle

Für eine Hypothese von Testmittelwert > Referenzmittelwert oder Testmittelwert – Referenzmittelwert > Untergrenze ist die 100(1 – α)%-Untergrenze gleich D_U.

Für eine Hypothese von Testmittelwert < Referenzmittelwert oder Testmittelwert – Referenzmittelwert < Obergrenze ist die 100(1 – α)%-Obergrenze gleich D_O.

Notation

Begriff	Beschreibung
D	Differenz zwischen dem Testmittelwert und dem Referenzmittelwert
SE	Standardfehler
δ1	Untere Äquivalenzgrenze
δ2	Obere Äquivalenzgrenze
v	Freiheitsgrade
α	Das Signifikanzniveau für den Test (Alpha)
t1-α, v	Oberer kritischer 1 – α-Wert für eine t-Verteilung mit v Freiheitsgraden

Es sei t₁ der t-Wert für die Hypothese, , und es sei t₂ der t-Wert für die Hypothese, , wobei die Differenz zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit ist. Die t-Werte werden standardmäßig wie folgt berechnet:

Für eine Hypothese von Testmittelwert > Referenzmittelwert, δ₁ = 0.

Für eine Hypothese von Testmittelwert < Referenzmittelwert, δ ₂ = 0.

Notation

Begriff	Beschreibung
D	Differenz zwischen dem Testmittelwert der Stichprobe und dem Referenzmittelwert der Stichprobe
SE	Standardfehler der Differenz
δ1	Untere Äquivalenzgrenze
δ2	Obere Äquivalenzgrenze

Die Wahrscheinlichkeit, P_H0, für jede Nullhypothese (H₀) wird wie folgt angegeben:

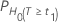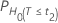Notation

Begriff	Beschreibung
	Unbekannte Differenz zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit
δ1	Untere Äquivalenzgrenze
δ2	Obere Äquivalenzgrenze
v	Freiheitsgrade
T	t-Verteilung mit v Freiheitsgraden
t1	t-Wert für die Hypothese
t2	t-Wert für die Hypothese