Ein Techniker bei einem Sehhilfeproduzenten testet eine neue Reinigungslösung für Kontaktlinsen. Der Techniker möchte feststellen, ob die neue Lösung Kontaktlinsen ebenso gut wie die führende Marke reinigt. Er lässt 14 Probanden Kontaktlinsen für einen Tag tragen und anschließend die Linsen reinigen. Jeder Proband reinigt eine Linse in der neuen Lösung und die andere in der Lösung der führenden Marke. Der Techniker bewertet die Sauberkeit der einzelnen Linsen durch Messen des Kontaktwinkels eines Flüssigkeitstropfens auf der Linse. Der Kontaktwinkel wird durch einen Film oder Rückstände auf der Linse beeinflusst. Damit Äquivalenz vorliegt, muss der mittlere Kontaktwinkel für die neue Lösung innerhalb von ±0,5 Grad dem mittleren Winkel der führenden Marke entsprechen.
Der Techniker führt einen Äquivalenztest bei verbundenen Stichproben durch, um zu bestimmen, ob die zwei Reinigungslösungen äquivalent sind.
- Öffnen Sie die Beispieldaten Kontaktlinsenreiniger.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Teststichprobe die Spalte Neu ein.
- Geben Sie im Feld Referenzstichprobe die Spalte Marktführer ein.
- Wählen Sie im Feld Hypothese zu den Wert Testmittelwert - Referenzmittelwert aus.
- Wählen Sie im Feld Was möchten Sie ermitteln? (Alternativhypothese) den Wert Untergrenze < Testmittelwert - Referenzmittelwert < Obergrenze aus.
- Geben Sie im Feld Untergrenze den Wert -0,5 ein.
- Geben Sie im Feld Obergrenze den Wert 0,5 ein.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
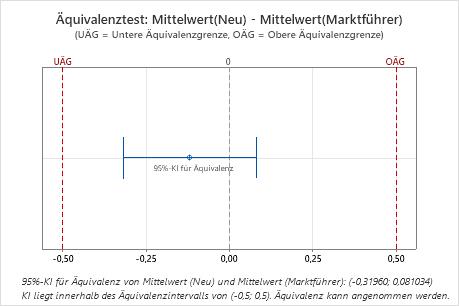
Da das Konfidenzintervall vollständig innerhalb des Äquivalenzintervalls liegt, schlussfolgert der Techniker, dass die zwei Reinigungslösungen äquivalent sind.
Methode
Referenzmittelwert = Mittelwert von Marktführer
Deskriptive Statistik
| Variable | N | Mittelwert | StdAbw | SE des Mittelwerts |
|---|---|---|---|---|
| Neu | 14 | 88,604 | 1,5578 | 0,41634 |
| Marktführer | 14 | 88,724 | 1,5907 | 0,42514 |
Differenz: Mittelwert(Neu) - Mittelwert(Marktführer)
| Differenz | StdAbw | SE | 95%-KI für Äquivalenz | Äquivalenzintervall |
|---|---|---|---|---|
| -0,11929 | 0,42324 | 0,11312 | (-0,319605; 0,0810335) | (-0,5; 0,5) |
Test
| Nullhypothese: | Differenz ≤ -0,5 oder Differenz ≥ 0,5 |
|---|---|
| Alternativhypothese: | -0,5 < Differenz < 0,5 |
| α-Niveau: | 0,05 |
| Nullhypothese | DF | t-Wert | p-Wert |
|---|---|---|---|
| Differenz ≤ -0,5 | 13 | 3,3657 | 0,003 |
| Differenz ≥ 0,5 | 13 | -5,4748 | 0,000 |