In diesem Thema
Differenz, Standardfehler und Standardabweichung innerhalb der Subjekte
Differenz
Die Differenz D für den Äquivalenztest wird wie folgt ausgedrückt:
SE
Der Standardfehler für die Differenz wird mit folgender Formel angegeben: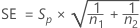
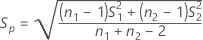
Standardabweichung innerhalb der Subjekte
Die Standardabweichung innerhalb der Subjekte Sw wird wie folgt ausgedrückt: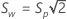
Notation
| Begriff | Beschreibung |
|---|---|
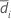 | Mittelwert der Stichprobe für Sequenz i (weitere Informationen finden Sie unter Methoden und Formeln für allgemeine Konzepte in Äquivalenztest, 2x2-Crossover-Versuchsplan) |
| ni | Anzahl der Teilnehmer in Sequenz i |
| Si | Standardabweichung der Stichprobe von 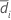 für Sequenz i für Sequenz i |
Konfidenzintervall
100(1 – α)%-KI
Standardmäßig wird das 100(1 – α)%-Konfidenzintervall (KI) für die Äquivalenz in Minitab mit der folgenden Formel berechnet:
KI = [min(C, Du), max(C, Do)]
Dabei gilt Folgendes:

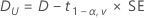
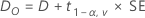
100(1 – 2α)%-KI
Wenn Sie die Option für die Verwendung des 100(1 – 2 α)%-KI auswählen, wird das KI mit der folgenden Formel angegeben:
KI = [Du, Do]
Einseitige Intervalle
Für eine Hypothese von Testmittelwert > Referenzmittelwert oder Testmittelwert – Referenzmittelwert > Untergrenze ist die 100(1 – α)%-Untergrenze gleich DU.
Für eine Hypothese von Testmittelwert < Referenzmittelwert oder Testmittelwert – Referenzmittelwert < Obergrenze ist die 100(1 – α)%-Obergrenze gleich DO.Notation
| Begriff | Beschreibung |
|---|---|
| D | Differenz zwischen dem Testmittelwert und dem Referenzmittelwert |
| SE | Standardfehler |
| δ1 | Untere Äquivalenzgrenze |
| δ2 | Obere Äquivalenzgrenze |
| v | Freiheitsgrade |
| α | Das Signifikanzniveau für den Test (Alpha) |
| t1-α, v | Oberer kritischer 1 – α-Wert für eine t-Verteilung mit v Freiheitsgraden |
t-Werte
 , und es sei t2 der t-Wert für die Hypothese,
, und es sei t2 der t-Wert für die Hypothese,  , wobei
, wobei  die Differenz zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit ist. Die t-Werte werden standardmäßig wie folgt berechnet:
die Differenz zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit ist. Die t-Werte werden standardmäßig wie folgt berechnet:


Für eine Hypothese von Testmittelwert > Referenzmittelwert, δ1 = 0.
Für eine Hypothese von Testmittelwert < Referenzmittelwert, δ 2 = 0.
Notation
| Begriff | Beschreibung |
|---|---|
| D | Differenz zwischen dem Testmittelwert der Stichprobe und dem Referenzmittelwert der Stichprobe |
| SE | Standardfehler der Differenz |
| δ1 | Untere Äquivalenzgrenze |
| δ2 | Obere Äquivalenzgrenze |
p-Werte
| H0 | p-Wert |
|---|---|
 |
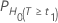 |
 |
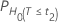 |
Notation
| Begriff | Beschreibung |
|---|---|
 | Unbekannte Differenz zwischen dem Mittelwert der Testgrundgesamtheit und dem Mittelwert der Referenzgrundgesamtheit |
| δ1 | Untere Äquivalenzgrenze |
| δ2 | Obere Äquivalenzgrenze |
| v | Freiheitsgrade |
| T | t-Verteilung mit v Freiheitsgraden |
| t1 | t-Wert für die Hypothese  |
| t2 | t-Wert für die Hypothese  |
Hinweis
Weitere Informationen zum Berechnen der t-Werte erhalten Sie im Abschnitt zu t-Werten.
