In diesem Thema
Gängige Notation
Bei allen Berechnungen für den Äquivalenztest für einen 2x2-Crossover-Versuchsplan wird angenommen, dass gemäß der Behandlungsreihenfolge für Sequenz 1 die Testbehandlung auf die Referenzbehandlung folgt und dass gemäß der Reihenfolge für Sequenz 2 die Referenzbehandlung auf die Testbehandlung folgt.
Sei Yijk die Antwortvariable für Teilnehmer k während der Periode j in Sequenz i, wobei i = 1, 2; j = 1, 2; k = 1 ... ni .
Wenn die Antwortvariable für eine Periode für einen Teilnehmer fehlt, werden die Daten für den betreffenden Teilnehmer in den Berechnungen ausgelassen.
d1k und d2k seien wie folgt definiert:
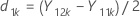
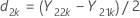
 und S1 stellen den Mittelwert der Stichprobe und die Standardabweichung der Stichprobe von d1k, k = 1, ..., n1 dar, angegeben durch folgende Formel:
und S1 stellen den Mittelwert der Stichprobe und die Standardabweichung der Stichprobe von d1k, k = 1, ..., n1 dar, angegeben durch folgende Formel:
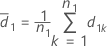
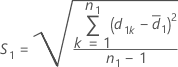
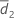 und S2 stellen den Mittelwert der Stichprobe und die Standardabweichung der Stichprobe von d2k, k = 1, ..., n2 dar, angegeben durch folgende Formel:
und S2 stellen den Mittelwert der Stichprobe und die Standardabweichung der Stichprobe von d2k, k = 1, ..., n2 dar, angegeben durch folgende Formel:
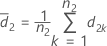
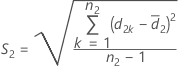
Notation
| Begriff | Beschreibung |
|---|---|
 | Mittelwert der Stichprobe von d1k, k = 1, ..., n1 |
| S1 | Standardabweichung der Stichprobe von d1k, k = 1, ..., n1 |
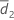 | Mittelwert der Stichprobe von d2k, k = 1, ..., n2 |
| S2 | Standardabweichung der Stichprobe von d2k, k = 1, ..., n2 |
Freiheitsgrade (DF)

Notation
| Begriff | Beschreibung |
|---|---|
| v | Freiheitsgrade |
| n1 | Anzahl der Teilnehmer in Sequenz 1 |
| n2 | Anzahl der Teilnehmer in Sequenz 2 |
Äquivalenzgrenzen
k1 sei die angegebene Untergrenze, k2 sei die angegebene Obergrenze. Die untere Äquivalenzgrenze δ1 wird standardmäßig mit der folgenden Formel angegeben:

Die obere Äquivalenzgrenze δ2 wird wie folgt angegeben:
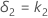
Wenn Sie jedoch die Option auswählen, mit der Ihre Grenzen mit dem Referenzmittelwert multipliziert werden, 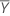 , werden die Grenzen mit folgender Formel angegeben:
, werden die Grenzen mit folgender Formel angegeben:


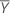 ist der Durchschnitt der durchschnittlichen Werte der Antwortvariablen für die zwei Referenzperioden.
ist der Durchschnitt der durchschnittlichen Werte der Antwortvariablen für die zwei Referenzperioden.
