In diesem Thema
Schritt 1: Bestimmen, ob der Testmittelwert und der Referenzmittelwert gleich sind
Vergleichen Sie das Konfidenzintervall mit den Äquivalenzgrenzen. Wenn das Konfidenzintervall vollständig innerhalb der Äquivalenzgrenzen liegt, können Sie annehmen, dass der Mittelwert der Testgrundgesamtheit gleich dem Mittelwert der Referenzgrundgesamtheit ist. Wenn ein Teil des Konfidenzintervalls außerhalb der Äquivalenzgrenzen liegt, kann keine Äquivalenz angenommen werden.
Differenz: Mittelwert(Rabatt) - Mittelwert(Original)
| Differenz | SE | 95%-KI für Äquivalenz | Äquivalenzintervall |
|---|---|---|---|
| -0,12122 | 0,20324 | (-0,483449; 0,241005) | (-0,5; 0,5) |
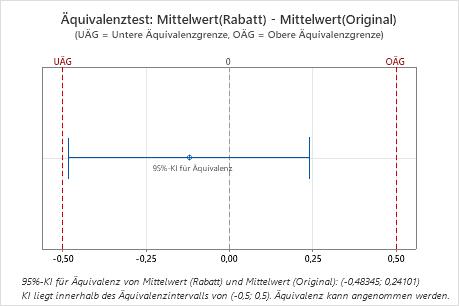
Wichtigste Ergebnisse: 95%-KI, Äquivalenzintervall
In diesen Ergebnissen liegt das 95%-Konfidenzintervall vollständig innerhalb des Äquivalenzintervalls, das durch die untere Äquivalenzgrenze (UÄG) und die obere Äquivalenzgrenze (OÄG) definiert wird. Daher können Sie annehmen, dass der Testmittelwert und der Referenzmittelwert äquivalent sind.
Hinweis
Sie können die Ergebnisse des Äquivalenztests auch mit Hilfe der p-Werte beurteilen. Zum Nachweis der Äquivalenz müssen die p-Werte für beide Nullhypothesen kleiner als Alpha sein.
Schritt 2: Prüfen der Daten auf Probleme
Probleme mit Ihren Daten, z. B. Schiefe oder Ausreißer, können die Ergebnisse beeinträchtigen. Suchen Sie anhand von Grafiken nach Schiefe (durch Untersuchen der Streubreite der Daten) und potenziellen Ausreißern.
Ermitteln, ob die Daten schief sind
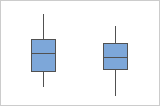
Wenn die Daten schief sind, liegen die meisten Datenwerte hin zum oberen oder unteren Rand der Grafik. Häufig lässt sich die Schiefe am einfachsten mit einem Boxplot oder einem Histogramm erkennen.
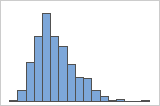
Rechtsschief
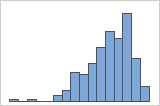
Linksschief
Das Histogramm mit rechtsschiefen Daten zeigt beispielsweise Gehaltsdaten. Viele Mitarbeiter erhalten ein relativ geringes Gehalt, während immer weniger Personen sehr hohe Gehälter beziehen. Das Histogramm mit linksschiefen Daten zeigt Daten zu Ausfallraten. Eine geringe Anzahl von Einheiten fällt früh aus, während immer mehr Einheiten zu einem späteren Zeitpunkt ausfallen.
Stark schiefe Daten können die Gültigkeit der Testergebnisse beeinträchtigen, wenn die Stichprobe klein ist (weniger als 20 Werte). Wenn die Daten stark schief sind und eine kleine Stichprobe vorliegt, erwägen Sie, den Stichprobenumfang zu vergrößern.
Identifizieren von Ausreißern
Ausreißer, d. h. Datenpunkte, die weit entfernt von den meisten anderen Datenwerten liegen, können sich stark auf die Ergebnisse auswirken. Ausreißer können am einfachsten in einem Boxplot identifiziert werden.
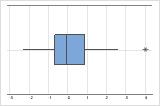
In einem Boxplot werden Ausreißer mit Sternchen (*) gekennzeichnet.
Versuchen Sie nach Möglichkeit, die Ursache von Ausreißern zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Daten zu entfernen, die auf Ausnahmebedingungen zurückzuführen sind, und die Analyse zu wiederholen. Weitere Informationen zu Ausnahmebedingungen finden Sie unter Verwenden von Regelkarten zum Erkennen von Streuung durch gewöhnliche Ursachen und Streuung durch Ausnahmebedingungen.
Vergleichen der Streubreite der Daten (optional)
Hinweis
Wenn Sie eine formale Prüfung auf gleiche Varianzen durchführen möchten, verwenden Sie Test auf Varianzen, 2 Stichproben.
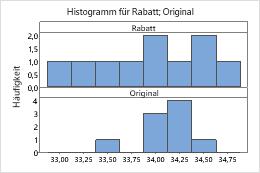
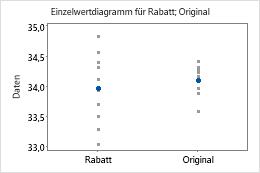
In diesen Grafiken scheinen die Daten nicht schief zu sein, und es sind keine Ausreißer vorhanden.
Die Streubreiten der Daten in der Testgruppe und der Referenzgruppe scheinen nicht gleich zu sein. Daher sollten Sie für den Test keine Gleichheit der Varianzen annehmen.
