Ein Lebensmitteltechniker für einen Tiernahrungshersteller testet eine neue, weniger teure Formulierung des beliebtesten Katzenfutters des Unternehmens. Der Techniker möchte sicherstellen, dass der Proteingehalt der billigeren Formulierung identisch mit dem Proteingehalt der ursprünglichen Formulierung ist. Er misst den Proteingehalt von 100-Gramm-Stichproben beider Formulierungen der Tiernahrung, um festzustellen, ob sie mit einer Toleranz von ±0,5 Gramm äquivalent sind.
Der Techniker führt einen Äquivalenztest bei zwei Stichproben durch, um zu bestimmen, ob die mittlere Differenz des Proteingehalts zwischen den beiden Formulierungen innerhalb einer Spannweite von ±0,5 g liegt. Dem Techniker ist nicht bekannt, ob die Varianzen des Proteingehalts für die beiden Formulierungen gleich sind.
- Öffnen Sie die Beispieldaten Katzenfutterprotein.MWX.
- Wählen Sie aus.
- Wählen Sie in der Dropdownliste die Option Stichproben aus verschiedenen Spalten aus.
- Geben Sie im Feld Teststichprobe die Spalte Rabatt ein.
- Geben Sie im Feld Referenzstichprobe die Spalte Original ein.
- Wählen Sie im Feld Hypothese zu den Wert Testmittelwert - Referenzmittelwert aus.
- Wählen Sie im Feld Was möchten Sie ermitteln? (Alternativhypothese) den Wert Untergrenze < Testmittelwert - Referenzmittelwert < Obergrenze aus.
- Geben Sie im Feld Untergrenze den Wert –0,5 ein.
- Geben Sie im Feld Obergrenze den Wert 0,5 ein.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
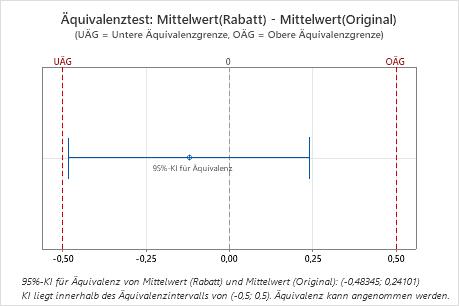
Da das Konfidenzintervall vollständig innerhalb des Äquivalenzintervalls liegt, schlussfolgert der Techniker, dass die zwei Formulierungen für Katzenfutter eine vergleichbare Menge an Protein enthalten.
Methode
Referenzmittelwert = Mittelwert von Original
Für die Analyse wurde nicht von gleichen Varianzen ausgegangen.
Deskriptive Statistik
| Variable | N | Mittelwert | StdAbw | SE des Mittelwerts |
|---|---|---|---|---|
| Rabatt | 10 | 33,971 | 0,58064 | 0,18361 |
| Original | 9 | 34,092 | 0,26138 | 0,087127 |
Differenz: Mittelwert(Rabatt) - Mittelwert(Original)
| Differenz | SE | 95%-KI für Äquivalenz | Äquivalenzintervall |
|---|---|---|---|
| -0,12122 | 0,20324 | (-0,483449; 0,241005) | (-0,5; 0,5) |
Test
| Nullhypothese: | Differenz ≤ -0,5 oder Differenz ≥ 0,5 |
|---|---|
| Alternativhypothese: | -0,5 < Differenz < 0,5 |
| α-Niveau: | 0,05 |
| Nullhypothese | DF | t-Wert | p-Wert |
|---|---|---|---|
| Differenz ≤ -0,5 | 12 | 1,8637 | 0,044 |
| Differenz ≥ 0,5 | 12 | -3,0566 | 0,005 |