In diesem Thema
Differenz
Bei der Differenz handelt es sich um die Differenz zwischen dem Stichprobenmittelwert und dem Sollwert.
Interpretation
Die Differenz der Stichprobendaten liefert einen Schätzwert für die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert.
Da die Differenz auf Stichprobendaten und nicht auf der kompletten Grundgesamtheit basiert, können Sie nicht sicher sein, dass sie gleich der Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert ist. Zum Bewerten der Präzision des Schätzwerts für die Grundgesamtheit können Sie ein Konfidenzintervall verwenden.
SE
Der Standardfehler (SE) der Differenz schätzt die Streuung der Differenz zwischen dem Soll und dem Stichprobenmittelwert, die Sie erhalten würden, wenn Sie wiederholt Stichproben aus derselben Grundgesamtheit ziehen. Mit dem Standardfehler der Differenz wird die Streuung zwischen Stichproben geschätzt, während mit der Standardabweichung die Streuung innerhalb einer Stichprobe gemessen wird.
Interpretation
Bestimmen Sie anhand des Standardfehlers der Differenz, wie präzise mit der Differenz zwischen dem Stichprobenmittelwert und dem Sollwert die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert geschätzt wird.
Niedrigere Werte des Standardfehlers zeigen einen präziseren Schätzwert an. Im Allgemeinen ergibt eine größere Standardabweichung einen größeren Standardfehler der Differenz und einen weniger präzisen Schätzwert. Ein größerer Stichprobenumfang ergibt einen kleineren Standardfehler der Differenz und einen präziseren Schätzwert.
In Minitab wird mit dem Standardfehler der Differenz die Teststatistik (t-Wert) berechnet.
Konfidenzintervall (KI)
Das Konfidenzintervall liefert einen Bereich wahrscheinlicher Werte für die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert. Die untere Konfidenzgrenze definiert einen Wert, den die Differenz wahrscheinlich überschreitet. Die obere Konfidenzgrenze definiert einen Wert, den die Differenz wahrscheinlich unterschreitet.
Hinweis
Wenn Sie beim Durchführen eines Äquivalenztests die Standardeinstellungen übernehmen, zeigt Minitab ein Konfidenzintervall für die Äquivalenz an. Wenn Sie die Standardeinstellung ändern und das Konfidenzintervall mit der Alternativmethode berechnen lassen, zeigt Minitab ein Standardkonfidenzintervall an. Weitere Informationen zum Unterschied zwischen diesen beiden Intervallen finden Sie unter Konfidenzintervalle in Äquivalenztests.
Interpretation
Vergleichen Sie das Konfidenzintervall mit den Äquivalenzgrenzen. Wenn das Konfidenzintervall vollständig innerhalb der Äquivalenzgrenzen liegt, können Sie annehmen, dass der Mittelwert der Grundgesamtheit gleich dem Sollwert ist. Wenn ein Teil des Konfidenzintervalls außerhalb der Äquivalenzgrenzen liegt, kann keine Äquivalenz angenommen werden.
Differenz: Mittelwert(Kraft) - Sollwert
| Differenz | SE | 95%-KI für Äquivalenz | Äquivalenzintervall |
|---|---|---|---|
| 0,28500 | 0,13831 | (0; 0,520586) | (-0,42; 0,42) |
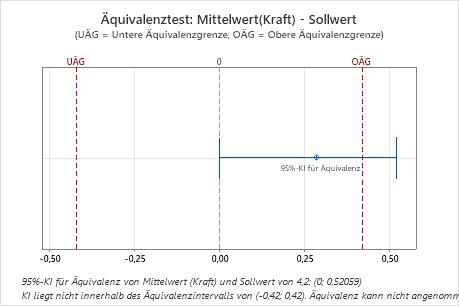
In diesen Ergebnissen überschreitet das 95%-Konfidenzintervall die obere Äquivalenzgrenze. Daher kann nicht angenommen werden, dass der Mittelwert der Grundgesamtheit und der Sollwert äquivalent sind.
Untergrenze
Wenn Sie eine Alternativhypothese auswählen, die nur eine Untergrenze für die Differenz enthält, wird in Minitab eine untere Konfidenzgrenze angezeigt. Die Untergrenze gibt einen Wert an, der von der Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert wahrscheinlich überschritten wird.
Interpretation
Bestimmen Sie anhand der unteren Konfidenzgrenze, ob die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert größer als die Untergrenze ist. Wenn die untere Konfidenzgrenze größer als die Untergrenze ist, können Sie schlussfolgern, dass die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert größer als die Untergrenze ist.
Differenz: Mittelwert(Kraft) - Sollwert
| Differenz | SE | Untere 95%-Grenze | Untergrenze |
|---|---|---|---|
| 0,28500 | 0,13831 | 0,049414 | -0,42000 |
In diesen Ergebnissen ist die untere 95%-Konfidenzgrenze für die Differenz gleich 0,04914 und somit größer als die Untergrenze von −0,4200. Daher können Sie zu 95 % sicher sein, dass die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert größer als die Untergrenze ist.
Obergrenze
Wenn Sie eine Alternativhypothese auswählen, die nur eine Obergrenze für die Differenz enthält, wird in Minitab eine obere Konfidenzgrenze angezeigt. Die Obergrenze gibt einen Wert an, der von der Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert wahrscheinlich unterschritten wird.
Interpretation
Bestimmen Sie anhand der oberen Konfidenzgrenze, ob die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert kleiner als die Obergrenze ist. Wenn die obere Konfidenzgrenze kleiner als die Obergrenze ist, können Sie schlussfolgern, dass die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert kleiner als die Obergrenze ist.
Differenz: Mittelwert(Kraft) - Sollwert
| Differenz | SE | Obere 95%-Grenze | Obergrenze |
|---|---|---|---|
| 0,28500 | 0,13831 | 0,52059 | 0,42000 |
In diesen Ergebnissen ist die obere 95%-Konfidenzgrenze gleich 0,52059 und damit größer als die Obergrenze von 0,4200. Daher können Sie nicht schlussfolgern, dass die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert kleiner als die Obergrenze ist.
Äquivalenzintervall
Ein Äquivalenzintervall ist ein Bereich von Werten, die ausreichend nah am Sollwert liegen, um als äquivalent erachtet zu werden. Das Intervall beruht auf Ihrer Kenntnis des Produkts bzw. des Prozesses, und es wird durch eine untere Äquivalenzgrenze (UÄG) und eine obere Äquivalenzgrenze (OÄG) definiert.
Interpretation
Vergleichen Sie das Konfidenzintervall mit den Äquivalenzgrenzen. Wenn das Konfidenzintervall vollständig innerhalb der Äquivalenzgrenzen liegt, können Sie annehmen, dass der Mittelwert der Grundgesamtheit gleich dem Sollwert ist. Wenn ein Teil des Konfidenzintervalls außerhalb der Äquivalenzgrenzen liegt, kann keine Äquivalenz angenommen werden.
Differenz: Mittelwert(Kraft) - Sollwert
| Differenz | SE | 95%-KI für Äquivalenz | Äquivalenzintervall |
|---|---|---|---|
| 0,28500 | 0,13831 | (0; 0,520586) | (-0,42; 0,42) |

In diesen Ergebnissen überschreitet das 95%-Konfidenzintervall die obere Äquivalenzgrenze. Daher kann nicht angenommen werden, dass der Mittelwert der Grundgesamtheit und der Sollwert äquivalent sind.
Untergrenze
Die untere Akzeptanzgrenze für die Differenz zwischen dem Mittelwert und dem Sollwert. Die Differenz zwischen dem Mittelwert der Testgrundgesamtheit und dem Sollwert soll größer als die Untergrenze sein.
Interpretation
Vergleichen Sie die Untergrenze mit der unteren Konfidenzgrenze. Wenn die untere Konfidenzgrenze größer als die Untergrenze ist, können Sie schlussfolgern, dass die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert größer als die Untergrenze ist.
Differenz: Mittelwert(Kraft) - Sollwert
| Differenz | SE | Untere 95%-Grenze | Untergrenze |
|---|---|---|---|
| 0,28500 | 0,13831 | 0,049414 | -0,42000 |
In diesen Ergebnissen ist die untere 95%-Konfidenzgrenze für die Differenz gleich 0,04914 und somit größer als die Untergrenze von −0,4200. Daher können Sie zu 95 % sicher sein, dass die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert größer als die Untergrenze ist.
Obergrenze
Die untere Akzeptanzgrenze für die Differenz zwischen dem Mittelwert und dem Sollwert. Die Differenz zwischen dem Mittelwert der Testgrundgesamtheit und dem Sollwert soll kleiner als die Obergrenze sein.
Interpretation
Vergleichen Sie die Obergrenze mit der oberen Konfidenzgrenze. Wenn die obere Konfidenzgrenze kleiner als die Obergrenze ist, können Sie schlussfolgern, dass die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert kleiner als die Obergrenze ist.
Differenz: Mittelwert(Kraft) - Sollwert
| Differenz | SE | Obere 95%-Grenze | Obergrenze |
|---|---|---|---|
| 0,28500 | 0,13831 | 0,52059 | 0,42000 |
In diesen Ergebnissen ist die obere 95%-Konfidenzgrenze gleich 0,52059 und damit größer als die Obergrenze von 0,4200. Daher können Sie nicht schlussfolgern, dass die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Sollwert kleiner als die Obergrenze ist.
