Ein Verpackungstechniker möchte ein neues Verfahren zum Versiegeln von Snackbeuteln testen. Die beim Öffnen der Beutel aufzuwendende Kraft muss innerhalb von 10 % des Sollwerts von 4,2 N (Newton) liegen. Der Techniker erfasst eine Zufallsstichprobe von 28 Beuteln, die mit dem neuen Verfahren versiegelt wurden, und zeichnet die Kraft auf, die beim Öffnen der Beutel aufgewendet werden muss.
Der Techniker führt einen Äquivalenztest bei einer Stichprobe durch, um zu bestimmen, ob die mittlere Kraft, die beim Öffnen von Beuteln mit der neuen Versiegelung aufgewendet werden muss, innerhalb von 10 % des Sollwerts von 4,2 N liegt.
- Öffnen Sie die Beispieldaten Snackbeutelversiegelung.MWX.
- Wählen Sie aus.
- Wählen Sie in der Dropdownliste die Option Stichprobe in einer Spalte aus.
- Geben Sie im Feld Stichprobe die Spalte Kraft ein.
- Geben Sie im Feld Soll den Wert 4,2 ein.
- Wählen Sie im Feld Was möchten Sie ermitteln? (Alternativhypothese) den Wert Untergrenze < Testmittelwert - Sollwert < Obergrenze aus.
- Geben Sie im Feld Untergrenze den Wert –0,1 ein.
- Geben Sie im Feld Obergrenze den Wert 0,1 ein.
- Wählen Sie Mit Sollwert multiplizieren aus.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
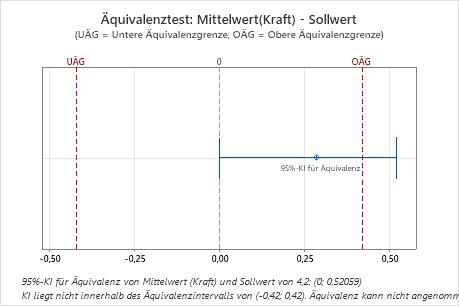
Das Konfidenzintervall liegt nicht vollständig innerhalb des Äquivalenzintervalls. Daher kann der Techniker nicht schlussfolgern, dass die beim Öffnen der Beutel mit der neuen Versiegelung aufzuwendende Kraft dem Sollwert von 4,2 N entspricht.
Methode
Untere Äquivalenzgrenze = -0,1 × Sollwert = -0,42
Obere Äquivalenzgrenze = 0,1 × Sollwert = 0,42
Deskriptive Statistik
| Variable | N | Mittelwert | StdAbw | SE des Mittelwerts |
|---|---|---|---|---|
| Kraft | 28 | 4,4850 | 0,73188 | 0,13831 |
Differenz: Mittelwert(Kraft) - Sollwert
| Differenz | SE | 95%-KI für Äquivalenz | Äquivalenzintervall |
|---|---|---|---|
| 0,28500 | 0,13831 | (0; 0,520586) | (-0,42; 0,42) |
Test
| Nullhypothese: | Differenz ≤ -0,42 oder Differenz ≥ 0,42 |
|---|---|
| Alternativhypothese: | -0,42 < Differenz < 0,42 |
| α-Niveau: | 0,05 |
| Nullhypothese | DF | t-Wert | p-Wert |
|---|---|---|---|
| Differenz ≤ -0,42 | 27 | 5,0972 | 0,000 |
| Differenz ≥ 0,42 | 27 | -0,97605 | 0,169 |