Was ist die Anderson-Darling-Statistik?
Anhand der Anderson-Darling-Statistik wird bestimmt, wie gut die Daten einer bestimmten Verteilung entsprechen. Für einen bestimmten Datensatz und eine bestimmte Verteilung gilt Folgendes: Je besser die Verteilung an die Daten angepasst ist, desto kleiner ist diese Statistik. Mit Hilfe der Anderson-Darling-Statistik können Sie beispielsweise ermitteln, ob die Daten die Annahme der Normalverteilung für einen t-Test erfüllen.
- H0: Die Daten folgen einer bestimmten Verteilung.
- H1: Die Daten folgen einer bestimmten Verteilung nicht.
Verwenden Sie den entsprechenden p-Wert (sofern verfügbar), um zu testen, ob die Daten aus der ausgewählten Verteilung stammen. Wenn der p-Wert kleiner als ein ausgewähltes Alpha-Niveau ist (normalerweise 0,05 oder 0,10), weisen Sie die Nullhypothese zurück, dass die Daten aus der betreffenden Verteilung stammen. Minitab zeigt für den Anderson-Darling-Test nicht immer einen p-Wert an, da dieser in bestimmten Fällen mathematisch nicht vorhanden ist.
Mit der Anderson-Darling-Statistik können Sie auch die Anpassung verschiedener Verteilungen vergleichen, um die beste Anpassung zu ermitteln. Um jedoch eine Schlussfolgerung hinsichtlich der besten Verteilung ziehen zu können, muss deren Anderson-Darling-Statistik wesentlich kleiner als die übrigen sein. Wenn die Statistiken nahe beieinander liegen, sollten Sie bei der Auswahl weitere Kriterien berücksichtigen, z. B. Wahrscheinlichkeitsnetze.
| Verteilung | Anderson-Darling | p-Wert |
|---|---|---|
| Exponential | 9,599 | p < 0,003 |
| Normal | 0,641 | p < 0,089 |
| Weibull mit 3 Parametern | 0,376 | p < 0,432 |
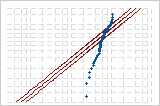
Exponential
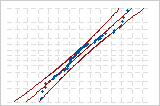
Normal
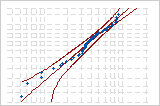
Weibull mit 3 Parametern
Beispiele für das Vergleichen von Statistiken
Diese Wahrscheinlichkeitsnetze wurden für dieselben Daten erstellt. Sowohl die Normalverteilung als auch die Weibull-Verteilung mit 3 Parametern bieten eine gute Anpassung an die vorliegenden Daten.
Minitab berechnet die Anderson-Darling-Statistik mit Hilfe der gewichteten quadrierten Distanz zwischen der Anpassungslinie des Wahrscheinlichkeitsnetzes (auf der Grundlage der ausgewählten Verteilung und mit der Maximum-Likelihood-Schätzmethode oder mit Schätzwerten der kleinsten Quadrate) und der verteilungsfreien Treppenfunktion. Die Berechnung ist in den Randbereichen der Verteilung stärker gewichtet.
Anzeigen der Anderson-Darling-Statistik in einem Wahrscheinlichkeitsnetz für Normalverteilung
So zeigen Sie eine Legende mit der Anderson-Darling-Teststatistik und dem p-Wert bei jedem Erstellen eines Wahrscheinlichkeitsnetzes für Normalverteilung der Residuen an:
- Wählen Sie und aus.
- Aktivieren Sie Anderson-Darling-Test mit Wahrscheinlichkeitsnetz einbinden. Klicken Sie auf OK. Minitab zeigt den Test nicht an, wenn weniger als drei Freiheitsgrade für Fehler vorhanden sind.
