Was sind Parameter, Parameterschätzwerte und Stichprobenverteilungen?

Wenn Sie Informationen zu einem bestimmten Merkmal der Grundgesamtheit (z. B. dem Mittelwert) ermitteln möchten, entnehmen Sie in der Regel eine Zufallsstichprobe aus dieser Grundgesamtheit, da es nicht möglich ist, die vollständige Grundgesamtheit zu messen. Auf der Grundlage dieser Stichprobe berechnen Sie das entsprechende Merkmal der Stichprobe, mit dem Informationen über das unbekannte Merkmal der Grundgesamtheit zusammengefasst wird. Das betreffende Merkmal der Grundgesamtheit wird als Parameter bezeichnet, das entsprechende Merkmal der Stichprobe als Stichprobenstatistik oder Parameterschätzwert. Da es sich bei der Statistik um eine Zusammenfassung von Informationen über einen Parameter handelt, der aus der Stichprobe gewonnen wurden, hängt der Wert der Statistik von der spezifischen Stichprobe ab, die aus der Grundgesamtheit entnommen wurde. Die Werte variieren zufällig von einer Zufallsstichprobe zur nächsten, und daher stellt die Statistik eine Zufallsmenge (Variable) dar. Die Wahrscheinlichkeitsverteilung dieser Zufallsvariable wird als Stichprobenverteilung bezeichnet. Die Stichprobenverteilung einer (Stichproben-)Statistik ist wichtig, weil sie es uns ermöglicht, auf der Grundlage einer Zufallsstichprobe Rückschlüsse über den entsprechenden Parameter der Grundgesamtheit zu ziehen.

Wenn wir z. B. eine Zufallsstichprobe aus einer normalverteilten Grundgesamtheit entnehmen, ist der Mittelwert der Stichprobe eine Statistik. Der anhand der vorliegenden Stichprobe bestimmte Mittelwert der Stichprobe ist ein Schätzwert des Mittelwerts der Grundgesamtheit. Dieser Schätzwert variiert zufällig, wenn aus derselben normalverteilten Grundgesamtheit eine andere Stichprobe entnommen wird. Die Wahrscheinlichkeitsverteilung, die diese Streuung beschreibt, ist die Stichprobenverteilung des Mittelwerts der Stichprobe. Die Stichprobenverteilung einer Statistik gibt alle möglichen Werte einer Statistik sowie die Häufigkeit an, mit der bestimmte Wertebereiche in der Statistik vorkommen. Wenn die übergeordnete Grundgesamtheit normalverteilt ist, ist die Stichprobenverteilung des Mittelwerts der Stichprobe ebenfalls normalverteilt.

Die folgenden Abschnitte enthalten weitere Informationen über Parameter, Parameterschätzwerte und Stichprobenverteilungen.

Informationen zu Parametern

Parameter sind deskriptive Maße einer vollständigen Grundgesamtheit, die als Eingaben für eine Dichtefunktion (PDF) verwendet werden können, um Verteilungskurven zu generieren. Parameter werden normalerweise durch griechische Buchstaben angegeben, um diese von Stichprobenstatistiken zu unterscheiden. Der Mittelwert der Grundgesamtheit wird beispielsweise mit dem griechischen Buchstaben Mu (μ) angegeben, die Standardabweichung der Grundgesamtheit mit dem griechischen Buchstaben Sigma (σ). Parameter sind feste Konstanten, d. h., im Gegensatz zu Variablen variieren sie nicht. Ihre Werte sind jedoch i. d. R. unbekannt, da es unmöglich ist, eine komplette Grundgesamtheit zu messen.

Jede Verteilung wird durch mehrere spezifische Parameter vollständig definiert; normalerweise handelt es sich hierbei um ein bis drei Parameter. Die folgende Tabelle enthält Beispiele für die Parameter, die für drei Verteilungen erforderlich sind. Die Parameterwerte bestimmen die Lage und Form der Kurve im Verteilungsdiagramm, und jede eindeutige Kombination von Parameterwerten ergibt eine eindeutige Verteilungskurve.

Verteilung	Parameter 1	Parameter 2	Parameter 3
Chi-Quadrat	Freiheitsgrade
Normal	Mittelwert	Standardabweichung
Gamma mit 3 Parametern	Form	Skala	Schwellenwert

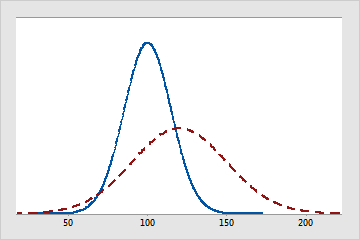
Eine Normalverteilung wird beispielsweise durch zwei Parameter definiert, den Mittelwert und die Standardabweichung. Wenn diese angegeben werden, ist die gesamte Verteilung genau bekannt.

Die durchgehende Linie stellt eine Normalverteilung mit einem Mittelwert von 100 und einer Standardabweichung von 15 dar. Die gestrichelte Linie zeigt ebenfalls eine Normalverteilung, diese weist jedoch eine Mittelwert von 120 und eine Standardabweichung von 30 auf.

Informationen zu Parameterschätzwerten (auch als Stichprobenstatistiken bezeichnet)

Parameter sind deskriptive Maße einer vollständigen Grundgesamtheit. Ihre Werte sind jedoch i. d. R. unbekannt, da es unmöglich ist, eine komplette Grundgesamtheit zu messen. Deshalb können Sie eine Zufallsstichprobe aus einer Grundgesamtheit entnehmen, um Parameterschätzwerte zu erhalten. Ein Ziel von statistischen Analysen ist es, Schätzwerte der Parameter einer Grundgesamtheit zusammen mit dem Fehlerbetrag zu erhalten, der mit diesen Schätzwerten verbunden ist. Diese Schätzwerte werden auch als Stichprobenstatistik bezeichnet.

Es gibt mehrere Typen von Parameterschätzwerten:

Punktschätzungen sind einzelne Werte eines Parameters, die am wahrscheinlichsten sind. Die Punktschätzung des Mittelwerts (des Parameters) einer Grundgesamtheit ist beispielsweise der Mittelwert der Stichprobe (der Parameterschätzwert).
Konfidenzintervalle sind Bereiche von Werten, die wahrscheinlich den Parameter der Grundgesamtheit enthalten.

Ein Beispiel für Parameterschätzwerte: Angenommen, Sie sind für einen Hersteller von Zündkerzen tätig, der ein Problem beim Elektrodenabstand untersucht. Es wäre zu kostspielig, jede einzelne hergestellte Zündkerze zu untersuchen. Sie entnehmen stattdessen eine Zufallsstichprobe von 100 Zündkerzen und messen den Abstand in Millimetern. Der Mittelwert der Stichprobe beträgt 9,2. Dies ist die Punktschätzung des Mittelwerts (μ) einer Grundgesamtheit. Sie erstellen außerdem ein 95%-Konfidenzintervall für μ, das (8,8; 9,6) lautet. Das bedeutet, dass Sie sich zu 95 % sicher sein können, dass der tatsächliche Wert des durchschnittlichen Abstands für alle Zündkerzen zwischen 8,8 und 9,6 liegt.

Informationen zu Stichprobenverteilungen

Eine Stichprobenverteilung ist die Wahrscheinlichkeitsverteilung einer bestimmten Statistik, z. B. des Mittelwerts. Um eine Stichprobenverteilung zu veranschaulichen, untersuchen wir ein einfaches Beispiel, bei dem die vollständige Grundgesamtheit bekannt ist. Die folgende Tabelle enthält beispielsweise die Gewichte einer vollständigen Grundgesamtheit von 6 Kürbissen. Die Kürbisse können jeweils nur einem der in der Tabelle aufgeführten Gewichte entsprechen.

Kürbis	1	2	3	4	5	6
Gewicht	19	14	15	12	16	17

Obwohl die vollständige Grundgesamtheit bekannt ist, untersuchen wir zu Illustrationszwecken alle möglichen Zufallsstichproben der Grundgesamtheit, die jeweils 3 Kürbisse enthalten (20 Zufallsstichproben). Dann berechnen wir für jede Stichprobe den Mittelwert. Die Stichprobenverteilung für den Stichprobenmittelwert wird von allen Stichprobenmittelwerten für jede mögliche Stichprobe von 3 Kürbissen beschrieben, wie in der folgenden Tabelle dargestellt.

Stichprobe	Gewichte	Mittleres Gewicht	Wahrscheinlichkeit
2, 3, 4	14, 15, 12	13,7	1/20
2, 4, 5	14, 12, 16	14	1/20
2, 4, 6	14, 12, 17	14,3	2/20
3, 4, 5	15, 12, 16	14,3	2/20
3, 4, 6	15, 12, 17	14,7	1/20
1, 2, 4	19, 14, 12	15	3/20
2, 3, 5	14, 15, 16
4, 5, 6	12, 16, 17
2, 3, 6	14, 15, 17	15,3	2/20
1, 3, 4	19, 15, 12	15,3	2/20
1, 4, 5	19, 12, 16	15,7	2/20
2, 5, 6	14, 16, 17	15,7	2/20
1, 2, 3	19, 14, 15	16	3/20
3, 5, 6	15, 16, 17
1, 4, 6	19, 12, 17
1, 2, 5	19, 14, 16	16,3	1/20
1, 2, 6	19, 14, 17	16,7	2/20
1, 3, 5	19, 15, 16	16,7	2/20
1, 3, 6	19, 15, 17	17	1/20
1, 5, 6	19, 16, 17	17,3	1/20

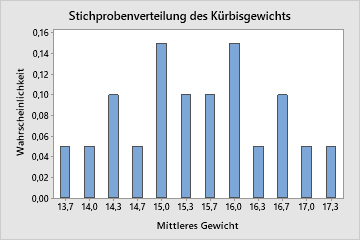
In dieser Grafik wird die Stichprobenverteilung des mittleren Gewichts gezeigt. Die Verteilung ist auf 15,5 zentriert, was dem tatsächlichen Mittelwert der Grundgesamtheit entspricht. Darüber hinaus weisen die Zufallsstichproben mit Mittelwerten, die näher an 15,5 liegen, eine höhere Wahrscheinlichkeit auf als Zufallsstichproben mit Mittelwerten, die weiter von 15,5 entfernt liegen.

In der Praxis ist es nicht praktikabel, die Verteilung der Stichprobenverteilung wie in dem obigen Beispiel tabellarisch darzustellen. Selbst im günstigsten Fall, wenn Sie die übergeordnete Grundgesamtheit Ihrer Stichproben kennen, sind Sie möglicherweise nicht in der Lage, die genaue Stichprobenverteilung der zu untersuchenden Stichprobenstatistik zu bestimmen. In einigen Fällen könnten Sie jedoch in der Lage sein, sich der Stichprobenverteilung der Stichprobenstatistik anzunähern. Wenn Sie z. B. eine Stichprobe aus einer normalverteilten Grundgesamtheit entnehmen, weist der Mittelwert der Stichprobe genau die Normalverteilung auf.

Wenn Sie jedoch eine Stichprobe aus einer nicht normalverteilten Grundgesamtheit entnehmen, sind Sie möglicherweise nicht in der Lage, die genaue Verteilung des Mittelwerts der Stichprobe zu bestimmen. Aufgrund des zentralen Grenzwertsatzes ist der Mittelwert der Stichprobe jedoch annähernd normalverteilt, sofern die Stichproben ausreichend groß sind. Wenn die Grundgesamtheit unbekannt ist und Ihre Stichproben groß genug sind, könnten Sie dann beispielsweise die Aussage treffen, dass der Mittelwert der Stichprobe mit einer Sicherheit von ca. 85 % innerhalb einer bestimmten Anzahl von Standardabweichungen vom Mittelwert der Grundgesamtheit liegt.