Der zentrale Grenzwertsatz ist ein grundlegender Satz der Wahrscheinlichkeitsrechnung und Statistik. Der Satz beschreibt die Verteilung des Mittelwerts einer zufälligen Stichprobe aus einer Grundgesamtheit mit endlicher Varianz. Bei ausreichend großem Stichprobenumfang ist die Verteilung der Mittelwerte etwa normalverteilt. Der Satz ist unabhängig von der Form der Grundgesamtheit gültig. Viele häufig verwendete statistische Prozeduren erfordern eine ungefähr normale Verteilung der Daten. Der zentrale Grenzwertsatz ermöglicht es jedoch, diese nützlichen Prozeduren auf Grundgesamtheiten anzuwenden, die stark von der Normalverteilung abweichen. Der erforderliche Stichprobenumfang hängt dabei von der Form der ursprünglichen Verteilung ab. Bei symmetrischer Verteilung der Grundgesamtheit kann ein Stichprobenumfang von 5 eine gute Approximation ergeben. Bei stark asymmetrischer Verteilung der Grundgesamtheit ist ein größerer Stichprobenumfang erforderlich. So könnte der Mittelwert beispielsweise ungefähr normalverteilt sein, wenn der Stichprobenumfang größer als 50 ist. Die folgenden Grafiken zeigen Beispiele dafür, wie sich die Verteilung auf den erforderlichen Stichprobenumfang auswirkt.
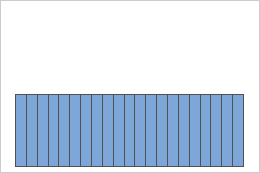
Gleichverteilung
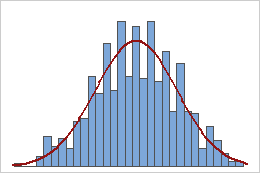
Stichprobenmittelwerte
Stichproben aus einer gleichverteilten Grundgesamtheit
Eine Grundgesamtheit, die einer Gleichverteilung folgt, ist symmetrisch, weicht jedoch stark von der Normalverteilung ab, wie das erste Histogramm verdeutlicht. Die Mittelwerte von 1000 Stichproben vom Umfang 5 in dieser Grundgesamtheit sind jedoch aufgrund des zentralen Grenzwertsatzes etwa normalverteilt, wie das zweite Histogramm verdeutlicht. Dieses Histogramm der Mittelwerte der Stichprobe enthält eine überlagerte Normalverteilungskurve, um die Normalität zu veranschaulichen.
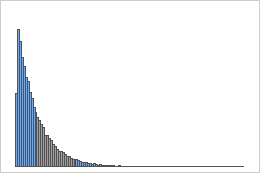
Exponentialverteilung
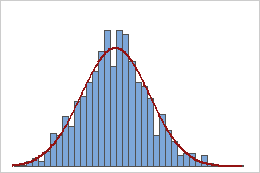
Stichprobenmittelwerte
Stichproben aus einer Exponentialverteilung
Eine Grundgesamtheit, die einer Exponentialverteilung folgt, ist asymmetrisch und nicht normalverteilt, wie das erste Histogramm verdeutlicht. Die Mittelwerte von 1000 Stichproben vom Umfang 50 in dieser Grundgesamtheit sind jedoch aufgrund des zentralen Grenzwertsatzes etwa normalverteilt, wie das zweite Histogramm verdeutlicht. Dieses Histogramm der Mittelwerte der Stichprobe enthält eine überlagerte Normalverteilungskurve, um die Normalität zu veranschaulichen.
