Ein kritischer Wert ist ein Punkt in der Verteilung der Teststatistik gemäß der Nullhypothese, der eine Menge von Werten definiert, die das Zurückweisen der Nullhypothese nahelegen. Diese Menge wird als kritischer oder Ablehnungsbereich bezeichnet. In der Regel weisen einseitige Tests einen kritischen Wert und zweiseitige Tests zwei kritische Werte auf. Die kritischen Werte werden so bestimmt, dass die Wahrscheinlichkeit, dass die Teststatistik einen Wert im Ablehnungsbereich des Tests aufweist, wenn die Nullhypothese wahr ist, dem Signifikanzniveau (als α oder Alpha bezeichnet) entspricht.
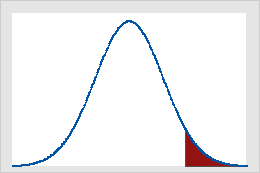
Abbildung A
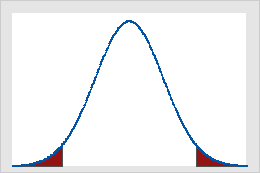
Abbildung B
Kritische Werte in der Standardnormalverteilung für α = 0,05
Abbildung A zeigt, dass die Ergebnisse eines einseitigen z-Tests signifikant sind, wenn der Wert der Teststatistik größer oder gleich 1,64 ist, dem kritischen Wert in diesem Fall. Der eingefärbte Bereich stellt die Wahrscheinlichkeit für einen Fehler 1. Art (α = 5 % in diesem Beispiel) für den Bereich unter der Kurve dar. Abbildung B zeigt, dass die Ergebnisse eines zweiseitigen z-Tests signifikant sind, wenn der Absolutwert der Teststatistik größer oder gleich 1,96 ist, dem kritischen Wert in diesem Fall. Die beiden eingefärbten Bereiche ergeben summiert 5 % (α) des Bereichs unter der Kurve.
Beispiele für das Berechnen von kritischen Werten
Bei Hypothesentests gibt es zwei Möglichkeiten, um zu bestimmen, ob die Stichprobe ausreichende Anzeichen dafür liefert, H0 zurückzuweisen oder H0 nicht zurückzuweisen. Die gängigste Möglichkeit besteht darin, den p-Wert mit einem vorab angegebenen Wert von α zu vergleichen. Dabei ist α die Wahrscheinlichkeit, dass H0 zurückgewiesen wird, wenn H0 wahr ist. Ein gleichwertiger Ansatz besteht jedoch darin, den auf der Grundlage Ihrer Daten berechneten Wert der Teststatistik mit dem kritischen Wert zu vergleichen. Im Folgenden finden Sie Beispiele zum Berechnen des kritischen Werts für einen t-Test bei einer Stichprobe und für eine einfache ANOVA.
Berechnen eines kritischen Werts für einen t-Test bei einer Stichprobe
- Wählen Sie aus.
- Wählen Sie Inverse kumulative Wahrscheinlichkeit aus.
- Geben Sie im Feld Freiheitsgrade den Wert 9 ein (Anzahl der Beobachtungen minus 1).
- Geben Sie im Feld Eingabekonstante den Wert 0,95 ein (1 minus 1/2 Alpha).
So erhalten Sie eine inverse kumulative Wahrscheinlichkeit (die dem kritischen Wert entspricht) von 1,83311. Wenn der Absolutwert der t-Statistik größer als dieser kritische Wert ist, können Sie die Nullhypothese H0 beim Signifikanzniveau 0,10 zurückweisen.
Berechnen eines kritischen Werts für eine Varianzanalyse (ANOVA)
- Wählen Sie aus.
- Wählen Sie Inverse kumulative Wahrscheinlichkeit aus.
- Geben Sie im Feld Freiheitsgrade des Zählers den Wert 2 ein (Anzahl der Faktorstufen minus 1).
- Geben Sie im Feld Freiheitsgrade des Nenners den Wert 9 ein (Freiheitsgrade für Fehler).
- Geben Sie im Feld Eingabekonstante den Wert 0,95 ein (1 minus Alpha).
Damit erhalten Sie eine inverse kumulative Wahrscheinlichkeit (einen kritischen Wert) von 4,25649. Ist die F-Statistik größer als dieser kritische Wert, können Sie die Nullhypothese H0 beim Signifikanzniveau 0,05 zurückweisen.
