Ein Konfidenzintervall ist ein Bereich von Werten, der statistisch aus einer Stichprobe abgeleitet wurde und wahrscheinlich den Wert eines unbekannten Parameters der Grundgesamtheit umfasst. Aufgrund ihrer zufälligen Natur ist es unwahrscheinlich, dass zwei Stichproben aus einer gegebenen Grundgesamtheit identische Konfidenzintervalle aufweisen. Wenn Sie die Stichprobennahme jedoch viele Male wiederholt haben, enthält ein bestimmter Prozentsatz der resultierenden Konfidenzintervalle den unbekannten Parameter der Grundgesamtheit.
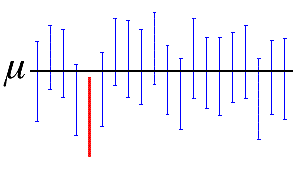
Hier stellt die horizontale schwarze Linie den festen Wert des unbekannten Mittelwerts µ der Grundgesamtheit dar. Die vertikalen blauen Konfidenzintervalle, die die horizontale Linie überlappen, enthalten den Mittelwert der Grundgesamtheit. Bei dem roten Konfidenzintervall, das komplett unterhalb der horizontalen Linie liegt, ist dies nicht der Fall. Ein 95%-Konfidenzintervall gibt an, dass 19 von 20 Stichproben (95 %) aus derselben Grundgesamtheit Konfidenzintervalle ergeben, die den Parameter der Grundgesamtheit enthalten.
Verwenden Sie das Konfidenzintervall, um den Schätzwert des Parameters der Grundgesamtheit zu beurteilen. Angenommen, ein Hersteller möchte ermitteln, ob die mittlere Länge der produzierten Bleistifte von der Solllänge abweicht. Der Hersteller nimmt eine Zufallsstichprobe der Bleistifte und ermittelt, dass die mittlere Länge der Stichprobe 52 Millimeter und das 95%-Konfidenzintervall (50,54) beträgt. Deshalb kann er sich zu 95 % sicher sein, dass die mittlere Länge aller Bleistifte zwischen 50 und 54 Millimeter beträgt.
- Punktschätzung
- Mit diesem einzelnen Wert wird der Parameter der Grundgesamtheit unter Verwendung der Stichprobendaten geschätzt.
- Fehlerspanne
-
Wenn Sie einen Wert mit Hilfe statistischer Verfahren schätzen, ist es wichtig zu beachten, dass der Schätzwert unabhängig von der Qualität des Analysedesigns einem Zufallsfehler unterliegt. Die Fehlerspanne quantifiziert diesen Fehler und gibt die Genauigkeit des Schätzwerts an.
Sie kennen wahrscheinlich bereits Fehlerspannen im Zusammenhang mit Umfrageergebnissen. Beispielsweise kann bei einer Wahlumfrage die Zustimmung zu einem Kandidaten mit 55 % bei einer Fehlerspanne von 5 % angegeben werden. Dies bedeutet, dass die tatsächliche Zustimmung um 5 % nach oben und unten abweichen kann und folglich zwischen 50 % und 60 % liegt.
Bei einem beidseitigen Konfidenzintervall ist die Fehlerspanne die Distanz zwischen dem geschätzten statistischen Wert und dem jeweiligen Wert des Konfidenzintervalls. Bei einem symmetrischen Konfidenzintervall beträgt die Fehlerspanne die Hälfte der Breite des Konfidenzintervalls. Beispiel: Die mittlere geschätzte Länge einer Nockenwelle ist 600 mm, und das Konfidenzintervall reicht von 599 bis 601. Somit ist die Fehlerspanne gleich 1.
Je größer die Fehlerspanne, desto größer das Intervall und desto geringer die Sicherheit über den Wert der Punktschätzung.
