Bei der Untersuchung der Beziehung zwischen zwei Variablen ist es wichtig, zu bestimmen, wie die Variablen zueinander in Beziehung stehen. Lineare Beziehungen kommen am häufigsten vor, aber Variablen können auch eine nichtlineare oder monotone Beziehung aufweisen, wie unten gezeigt. Es ist auch möglich, dass es keine Beziehung zwischen den Variablen gibt. Am besten beginnen Sie damit, ein Streudiagramm der Variablen zu erstellen, um die Beziehung zu untersuchen.
Eine lineare Beziehung ist ein Trend in den Daten, der durch eine gerade Linie modelliert werden kann. Angenommen, eine Fluggesellschaft möchte die Auswirkungen der Treibstoffpreise auf die Flugkosten schätzen. Es wird festgestellt, dass die Kosten eines Flugs zwischen Los Angeles und New York mit jedem Dollar, der für eine Gallone Flugzeugtreibstoff mehr bezahlt werden muss, um 3500 US$ steigen. Dies beschreibt eine lineare Beziehung zwischen den Kosten für Flugzeugtreibstoff und den Flugkosten.
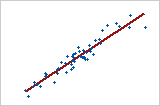
Diagramm 1: Starke positive lineare Beziehung
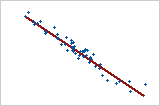
Diagramm 2: Starke negative lineare Beziehung
Wenn beide Variablen gleichzeitig und mit einer konstanten Rate steigen oder fallen, liegt eine positive lineare Beziehung vor. Die Punkte in Diagramm 1 folgen der Linie eng, was auf eine starke Beziehung zwischen den Variablen hindeutet. Der Korrelationskoeffizient nach Pearson für diese Beziehung ist +0,921.
Wenn eine Variable steigt und die andere gleichzeitig fällt, liegt eine negative lineare Beziehung vor. Die Punkte in Diagramm 2 folgen der Linie eng, was auf eine starke Beziehung zwischen den Variablen hindeutet. Der Korrelationskoeffizient nach Pearson für diese Beziehung ist −0,968.
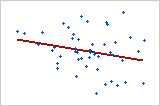
Diagramm 3: Schwache lineare Beziehung
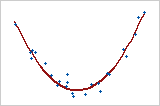
Diagramm 4: Nichtlineare Beziehung
Die Datenpunkte in Diagramm 3 scheinen zufällig verteilt zu sein. Sie liegen nicht eng an der Linie an, was auf eine sehr schwache Beziehung hindeutet, falls überhaupt eine Beziehung vorhanden ist. Der Korrelationskoeffizient nach Pearson für diese Beziehung ist -0,253.
Wenn eine Beziehung zwischen zwei Variablen nicht linear ist, kann sich die Rate der Zunahme oder Abnahme gleichzeitig mit den Änderungen in den Werten einer Variablen ändern und zu einem gekrümmten Muster in den Daten führen. Dieser Krümmungstrend kann möglicherweise besser mit einer nichtlinearen Funktion modelliert werden, z. B. mit einer quadratischen oder kubischen Funktion, oder die Beziehung wird durch eine Transformation linear gemacht. Diagramm 4 veranschaulicht eine starke Beziehung zwischen den Variablen. Da jedoch keine lineare Beziehung vorliegt, ist der Korrelationskoeffizient nach Pearson lediglich +0,244. Dies zeigt, warum es wichtig ist, die Daten grafisch darzustellen, um mögliche Beziehungen untersuchen zu können.
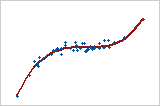
Diagramm 5: Monotone Beziehung
In einer monotonen Beziehung bewegen sich die Variablen tendenziell in dieselbe relative Richtung, aber nicht zwangsläufig mit einer konstanten Rate. In einer linearen Beziehung bewegen sich die Variablen mit einer konstanten Rate in dieselbe Richtung. Diagramm 5 zeigt, dass beide Variablen gleichzeitig zunehmen, jedoch nicht mit der gleichen Rate. Diese Beziehung ist monoton, aber nicht linear. Der Korrelationseffizient nach Pearson für diese Daten ist 0,843, doch der Korrelationseffizient nach Spearman ist mit 0,948 höher.
Lineare Beziehungen sind auch monoton. So ist die in Diagramm 1 dargestellte Beziehung sowohl monoton als auch linear.
